VH
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 4 2020
Bài 1:
Gọi 2 số là a,b (\(a,b\inℤ\))
Ta có: a+b=51(*)
Mà 2/5a=1/6b
=> a=5/12b
Thay vào (*) ta có: 17/12b=51
=>b=36
PN
28 tháng 5 2020
Bài 1 :
Gọi số thứ nhất và số thứ hai lần lượt là x và y (x,y thuộc z)
Tổng hai số bằng : \(x+y=51\left(1\right)\)
Biết 2/5 số thứ nhất thì bằng 1/6 số thứ hai
\(x\frac{2}{5}-y\frac{1}{6}=0\left(2\right)\)
Từ 1 và 2 ta suy ra được hệ phương trình sau :
\(\hept{\begin{cases}x+y=51\\x\frac{2}{5}-y\frac{1}{6}=0\end{cases}}\)\(< =>\hept{\begin{cases}x=51-y\\\frac{2x}{5}-\frac{y}{6}=0\end{cases}}\)
\(< =>\frac{\left(51-y\right)2}{5}-\frac{y}{6}=0\)\(< =>\frac{102-2y}{5}-\frac{y}{6}=0\)
\(< =>\frac{102-2y}{5}=\frac{y}{6}\)\(< =>\left(102-2y\right)6=5y\)
\(< =>612-12y=5y\)\(< =>612=17y\)
\(< =>y=\frac{612}{17}=36\left(3\right)\)
Thay 3 vào 1 ta được : \(x+y=51\)
\(< =>x+36=51< =>x=51-36=15\)
Vậy số thứ nhất và số thứ hai lần lượt là 15 và 36
PT
1
CM
5 tháng 6 2017
Gọi số thứ nhất là x (x < 51)
Số thứ hai là 51 – x
Theo điều kiện đề bài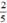 
số thứ nhất bằng 
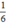số thứ hai nên ta có phương trình:
TD
7 tháng 5 2021
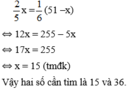
Gọi số thứ hai là x. Vậy số thứ nhất là 3x.
Vì tổng của chúng bằng 32 nên ta có phương trình x+3x=32 suy ra x=8.
Vậy số thứ nhất là 24 và số thứ hai là 8
TT
1
12 tháng 6 2018
Gọi số thứ nhất là a (a thuộc N);
=> Số thứ 2 là 458-a
Ta có 5a/6 +(458-a)/4=251
=> 5a/6+114,5- a/4=251
=> 10a/12-3a/12=136,5
=>7a/12=136,5
=> a= 234
=> 458-a=224
18 tháng 1 2019
a, Gọi chữ số hàng chục của số đó là a (\(0\le a< 6\))
Khi đó chữ số hàng đơn vị của số là 6-a.
Theo đề bài, ta có:
\(\overline{\left(6-a\right)a}-\overline{a\left(6-a\right)}=18\\ \Leftrightarrow10\left(6-a\right)+a-\left[10a-6+a\right]=18\\ \Leftrightarrow60-10a+a-9a-6=18\\ \Leftrightarrow18a=36\\ \Leftrightarrow a=2\)
Vậy số cần tìm là: 24.
b, Gọi 2 số trên lần lượt là a và b.
Theo đề bài, ta có:
\(\dfrac{2}{5}a=\dfrac{1}{6}b\Leftrightarrow b=\dfrac{12}{5}a\)
Mà \(a+b=51\) nên:
\(a+\dfrac{12}{5}a=51\\ \Leftrightarrow\dfrac{17}{5}a=51\\ \Leftrightarrow a=15\)
Do đó:
\(b=51-a=51-15=36\)
Vậy phân số cần tìm (really!?) là \(\dfrac{15}{36}\).
Chúc bạn học tốt nha
20 tháng 12 2022
Câu 2:
Gọi hai số cần tìm lần lượt là a,b
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=51\\\dfrac{2}{5}a=\dfrac{1}{6}b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=15\\b=36\end{matrix}\right.\)
PA
1
Thử:
Gọi 2/5 stn=1/6 sth = x
=> stn=5x/2 ; sth=6x
stn+sth=17x/2=51
x=51:17x2=6
Vậy stn=5x/2=15 ; sth=6x=36
Gọi st1 là x
Số t2 la : 51-x
Theo đề bài ta có pt: \(\frac{2}{5}x=\frac{1}{6}\left(51-x\right)\)
\(\Leftrightarrow\) \(\frac{2}{5}x=\frac{17}{2}-\frac{1}{6}x\)
\(\Leftrightarrow\) \(\frac{2}{5}x+\frac{1}{6}x=\frac{17}{2}\)
\(\Leftrightarrow\) \(\frac{17}{30}x=\frac{17}{2}\)
\(\Leftrightarrow\) \(x=15\)
Vậy :...................................