
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL :
Tổng ba góc của một tam giác bằng 1800
Chúc bn hok tốt ~

Các tính chất ở cá câu a ,b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180o".
Tính chất ở câu c được suy ra từ định lí "Trong một tam giác cân hai góc ở đáy bằng nhau".
Tính chất ở câu d được suy ra từ định lí: Nếu một tam giác có ba góc bằng nhau thì tam giác đo là tam giác cân.
Các tính chất ở các câu (a); (b) được suy ra từ định lí: “Tổng ba góc của một tam giác bằng nhau bằng 1800”.
Tính chất ở câu (c) được suy ra từ định lí: “Trong tam giác cân, hai góc ở đáy bằng nhau”.
Tính chất ở câu (d) được suy ra từ định lí: “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”.

Ta có :
Tổng ba góc của tam giác ABC bằng 180o nên ∠A + ∠B = 180o - ∠C
Góc ACx là góc ngoài của tam giác ABC nên ∠(ACx) = 180o - ∠C
Do đó : ∠(ACx) = ∠A + ∠B

Tổng số đo ba góc của tam giác MNP bằng 180o.
=> Tổng ba góc của một tam giác bất kì bằng 180o.

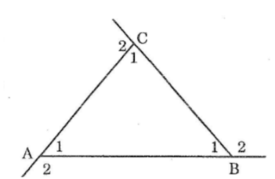
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)
∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)
∠(C1 ) +∠(C2 )=180o(hai góc kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
360 độ