VV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
2
HH
30 tháng 6 2020
A E B H D G F C
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật
<=> EH ⊥ EF
<=>\(AC\perp BD\) (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
<=>EF = EH
<=> AC = BD (Vì \(EF=\frac{AC}{2},EH=\frac{BD}{2}\))
c) EFGH là hình vuông
<=> EFGH là hình thoi và EFGH là hình chữ nhật
<=> AC = BD và .\(AC\perp DB\)
đố làm được ha
25 tháng 8 2021
c: Ta có: \(EF\le KE+KF\)
\(\Leftrightarrow EF\le\dfrac{DC+AB}{2}\)
Dấu '='xảy ra khi E,K,F thẳng hàng
hay EF//AB//DC
Suy ra: ABCD là hình thang
8 tháng 10 2019
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
8 tháng 10 2019
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
TB
4
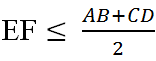
Số ban đầu là: 48