Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{2015.2017}\)
\(A=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2015}-\dfrac{1}{2017}\)
\(A=1-\dfrac{1}{2017}=\dfrac{2016}{2017}\)
\(B=\dfrac{3}{1.4}+\dfrac{3}{5.7}+\dfrac{3}{7.10}+...+\dfrac{3}{100.103}\)
\(B=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{100}-\dfrac{1}{103}\)
\(B=1-\dfrac{1}{103}=\dfrac{102}{103}\)
\(C=\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{62.65}\)
\(3C=3\left(\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{62.65}\right)\)
\(3C=\dfrac{3}{2.5}+\dfrac{3}{5.8}+\dfrac{3}{8.11}+...+\dfrac{3}{62.65}\)
\(3C=\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{62}-\dfrac{1}{65}\)
\(3C=\dfrac{1}{2}-\dfrac{1}{65}\)
\(3C=\dfrac{63}{130}\)
\(C=\dfrac{63}{130}:3=\dfrac{21}{130}\)

Câu 2:
\(D=\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{100}{101}=\dfrac{150}{101}\)
Câu 3:
\(E=2\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{205}-\dfrac{1}{207}\right)\)
\(=2\cdot\left(1-\dfrac{1}{207}\right)=2\cdot\dfrac{206}{207}=\dfrac{412}{207}\)
Câu 5:
\(G=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{17}\right)\)
\(=\dfrac{1}{4}\cdot\dfrac{16}{17}=\dfrac{4}{17}\)

a)\(P=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+...+\frac{1}{46}-\frac{1}{56}\)
=\(1-\frac{1}{56}=\frac{55}{56}\)
b)\(A.\frac{1}{3}=\frac{1}{3}.\left(\frac{3}{1.2}+\frac{3}{2.3}+....+\frac{3}{99.100}\right)\)
= \(\frac{1}{3}A=\frac{1}{1.2}+\frac{1}{2.3}+....+\frac{3}{99.100}\)
=> \(\frac{1}{3}A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\)
=> \(\frac{1}{3}A=1-\frac{1}{100}=\frac{99}{100}\)
=> \(A=\frac{99}{100}.3=\frac{297}{100}\)
c)\(B=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+...+\frac{1}{100}-\frac{1}{103}\)
=\(1-\frac{1}{103}=\frac{102}{103}\)
d) \(\frac{3}{5}C=\frac{3}{5}.\left(\frac{5}{1.4}+\frac{5}{4.7}+...+\frac{5}{100.103}\right)\)
=\(\frac{3}{1.4}+\frac{3}{4.7}+...+\frac{3}{100.103}\)
=\(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+....+\frac{1}{100}-\frac{1}{103}\)
=\(1-\frac{1}{103}=\frac{102}{103}\)
=>\(C=\frac{102}{103}.\frac{5}{3}=\frac{170}{103}\)
e) \(\frac{4}{7}D=\frac{4}{7}.\left(\frac{7}{1.5}+\frac{7}{5.9}+...+\frac{7}{101.105}\right)\)
=\(\frac{4}{1.5}+\frac{4}{5.9}+...+\frac{4}{101.105}\)
=\(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+...+\frac{1}{101}-\frac{1}{105}\)
=\(1-\frac{1}{105}=\frac{104}{105}\)
=< D=\(\frac{104}{105}.\frac{7}{4}=\frac{26}{15}\)

a)Đặt \(A=\dfrac{6}{1.4}+\dfrac{6}{4.7}+\dfrac{6}{7.10}+...+\dfrac{6}{97.100}\)
\(3a=3-\dfrac{3}{4}+\dfrac{3}{4}-\dfrac{3}{7}+\dfrac{3}{7}-\dfrac{3}{10}+...+\dfrac{3}{97}-\dfrac{3}{100}\)
\(=3-\dfrac{3}{100}\)
\(=\dfrac{297}{100}\)
b)Đặt \(B=\dfrac{4}{1.3}+\dfrac{16}{3.5}+\dfrac{36}{5.7}+...+\dfrac{9604}{97.99}\)
\(=2b=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{97.99}\)
\(2b=2-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{5}+\dfrac{2}{5}-\dfrac{2}{7}+...+\dfrac{2}{97}-\dfrac{2}{99}\)
\(2b=2-\dfrac{2}{99}=\dfrac{198}{99}-\dfrac{2}{99}=\dfrac{196}{99}\)
c) Tương tự! Bạn tự làm nhé!

Bài 1 :
\(S=1.3+3.5+5.7+...+99.101=3+15+35+...9999\)
Ta thấy :
\(3=2^2-1\)
\(15=4^2-1\)
\(35=6^2-1\)
.....
\(9999=100^2-1\)
\(\Rightarrow S=2^2+4^2+...+100^2-\left(1\right).\left(\left(100-2\right):2+1\right)\)
\(\Rightarrow S=\dfrac{100.\left(100+1\right)\left(2.100+1\right)}{6}-51\)
\(\Rightarrow S=\dfrac{100.101.201}{6}-51=338299\)

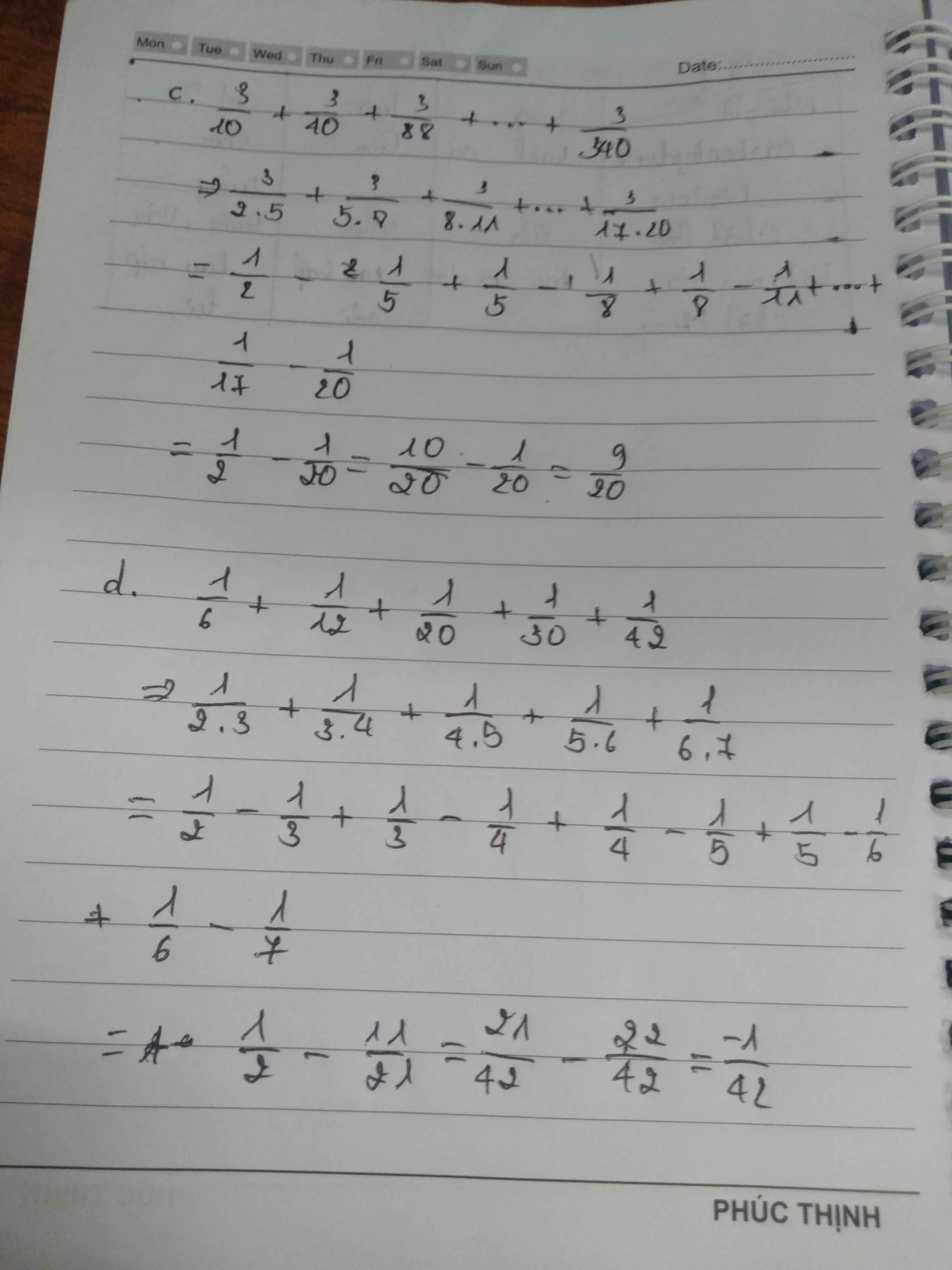
\(A=\frac{3}{1.4}+\frac{3}{4.7}+..........+\frac{3}{91.94}\)
\(\Leftrightarrow A=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+.....+\frac{1}{91}-\frac{1}{94}\)
\(\Leftrightarrow A=1-\frac{1}{94}=\frac{93}{94}\)
\(B=\frac{1}{1.3}+\frac{1}{3.5}+......+\frac{1}{97.99}\)
\(\Leftrightarrow2B=\frac{2}{1.3}+\frac{2}{3.5}+.......+\frac{3}{97.99}\)
\(\Leftrightarrow2B=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+.....+\frac{1}{97}-\frac{1}{99}\)
\(\Leftrightarrow2B=1-\frac{1}{99}=\frac{98}{99}\)
\(\Leftrightarrow B=\frac{98}{99}:2=\frac{49}{99}\)
Ta có : \(A=\frac{3}{1.4}+\frac{3}{4.7}+.....+\frac{3}{91.94}\)
\(=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+.....+\frac{1}{91}-\frac{1}{94}\)
\(=1-\frac{1}{94}\)
\(=\frac{93}{94}\)