
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500

Bài 1:
e; \(\dfrac{10}{21}\) - \(\dfrac{3}{8}\) : \(\dfrac{15}{4}\)
= \(\dfrac{10}{21}\) - \(\dfrac{3}{8}\) x \(\dfrac{4}{15}\)
= \(\dfrac{10}{21}\) - \(\dfrac{1}{10}\)
= \(\dfrac{100}{210}\) - \(\dfrac{21}{210}\)
= \(\dfrac{79}{210}\)
f; (\(\dfrac{2}{3}\) + \(\dfrac{3}{4}\)).(\(\dfrac{5}{7}\) + \(\dfrac{5}{14}\))
= (\(\dfrac{8}{12}\) + \(\dfrac{9}{12}\)).(\(\dfrac{10}{14}\) + \(\dfrac{5}{14}\))
= \(\dfrac{17}{12}\).\(\dfrac{15}{14}\)
= \(\dfrac{85}{56}\)

Ta có các quy luật sau:
\(\left(1+3\right)-2=2\)
\(\left(2+2\right)-3=1\)
\(\left(5+5\right)-6=4\)
Vậy dòng cuối là:
\(\left(5+9\right)-5=9\)
Số điền vào là 9
(Quy luật: lấy 2 số phía dưới cộng với nhau rồi trừ cho số phía trên sẽ ra được số ở giữa)

Quy luật: Hiệu của số lớn hơn trừ cho số nhỏ hơn trong mổi ô chính là kết quả của ô màu vàng đối diện
17-13=4
15-6=9
14-8=6
19-12=7
23-15=8
27-25=2
23-18=5
Suy ra: 12-x=3
=> x=12-3=9
Đáp án C
Giải thích: Mỗi số trong hình tam giác màu vàng bằng số lớn hơn của hình bình hành đối diện trừ đi số bé hơn ở hình bình hành đối diện.
=> ? - 12 = 3 hoặc 12 - ? = 3
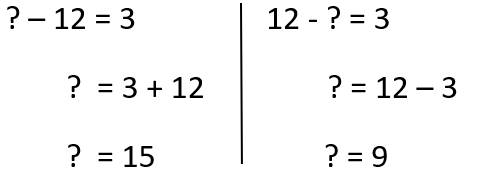
=> Đáp án là 15 hoặc 9
Đáp án: c
Bổ sung: Đáp án cũng có thể là 15

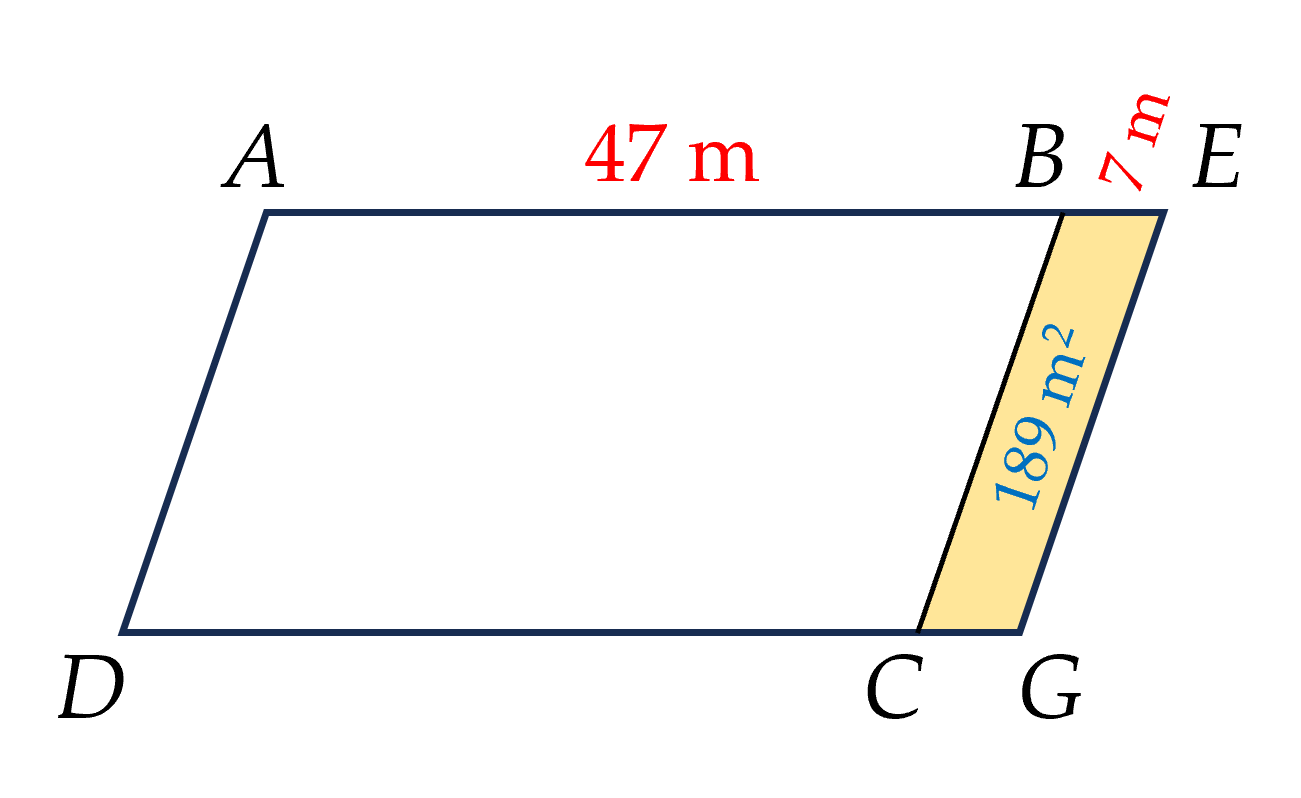
Đường cao hình bình hành là :
189 : 7 = 27 (m)
Diện tích hbh ban đầu là :
27 x 47 = 1269(m^2)

\(\frac{6}{x}=\frac{24}{x-27}\)
=> 6.( x - 27 ) = 24x
=> 6x - 162 = 24x
=> 162 = 6x - 24x
=> 162 = -18x
=> x = 162 : (-18)
=> x = -9

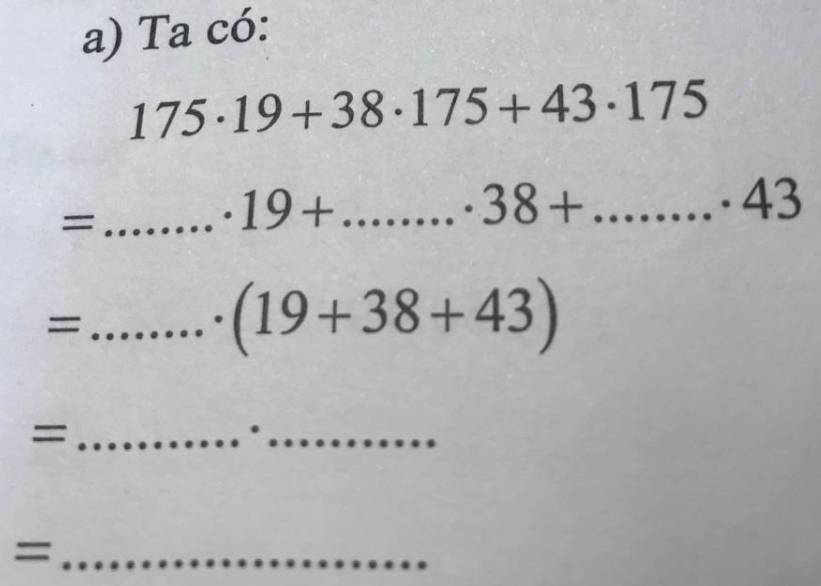
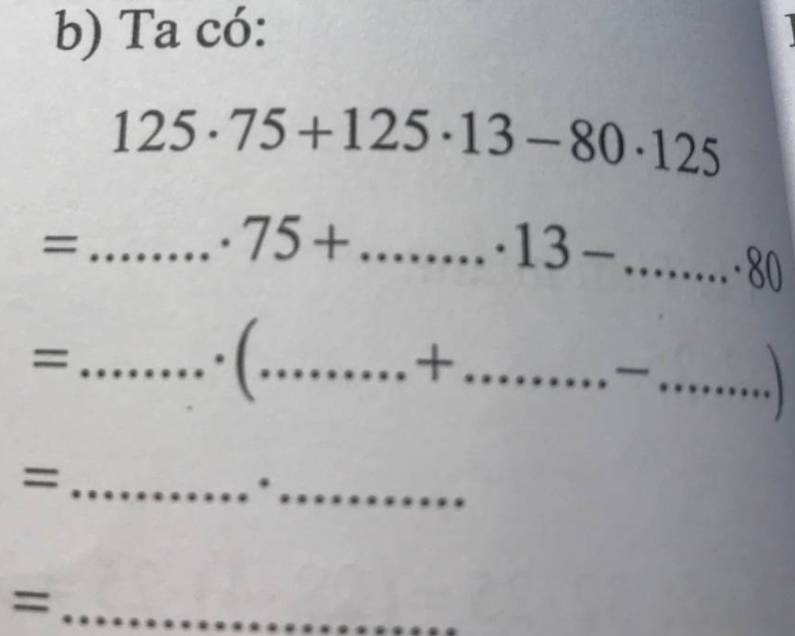











 Lun vui tươi như vậy ha!!
Lun vui tươi như vậy ha!! 







bài 6 làm như thế nào hả các bạn
Bài 1:
\(A=-\frac25+\frac34\cdot\frac29\)
\(=-\frac25+\frac{6}{36}\)
\(=-\frac25+\frac16=-\frac{12}{30}+\frac{5}{30}=-\frac{7}{30}\)
\(B=\frac38\cdot\frac{-13}{15}-\frac38\cdot\frac{2}{15}+1\frac12\)
\(=\frac38\left(-\frac{13}{15}-\frac{2}{15}\right)+\frac32\)
\(=-\frac38+\frac32=-\frac38+\frac{12}{8}=\frac98\)
\(C=-\frac78+\frac{9}{10}\cdot\frac23\)
\(=-\frac78+\frac93\cdot\frac{2}{10}\)
\(=-\frac78+\frac35=-\frac{35}{40}+\frac{24}{40}=-\frac{11}{40}\)
\(D=\frac{5}{11}\cdot\frac{-17}{31}-\frac{5}{11}\cdot\frac{14}{31}+1\frac12\)
\(=-\frac{5}{11}\left(\frac{17}{31}+\frac{14}{31}\right)+\frac32\)
\(=-\frac{5}{11}+\frac32=-\frac{10}{22}+\frac{33}{22}=\frac{23}{22}\)
Bài 2:
a: \(\frac65-\frac15\cdot\frac{10}{3}\)
\(=\frac65-\frac{10}{5}\cdot\frac13=\frac65-\frac23\)
\(=\frac{18}{15}-\frac{10}{15}=\frac{8}{15}\)
b: \(\frac{11}{24}-\frac{5}{41}+\frac{13}{24}+0,5-\frac{36}{41}\)
\(=\left(\frac{11}{24}+\frac{13}{24}\right)-\left(\frac{5}{41}+\frac{36}{41}\right)+0,5\)
\(=1-1+0,5=0,5\)
c: \(\frac12\cdot\frac{-3}{4}+\frac12\cdot\frac{-1}{4}+\frac23\)
\(=\frac12\left(-\frac34-\frac14\right)+\frac23\)
\(=-\frac12+\frac23=-\frac36+\frac46=\frac16\)
d: \(\frac13\cdot\frac{-5}{6}+\frac13\cdot\frac{-1}{6}+\frac12\)
\(=\frac13\left(-\frac56-\frac16\right)+\frac12\)
\(=-\frac13+\frac12=\frac16\)
Bài 3:
a: \(\frac{6}{x-7}=\frac{-3}{7}\)
=>\(\frac{6}{x-7}=\frac{-6}{14}\)
=>x-7=-14
=>x=-14+7=-7
b: \(-\frac35-x=\frac12\)
=>\(x=-\frac35-\frac12=-\frac{6}{10}-\frac{5}{10}=-\frac{11}{10}\)
c: \(x-\frac{3}{10}=\frac{7}{15}\cdot\frac{3}{14}\)
=>\(x-\frac{3}{10}=\frac{7}{14}\cdot\frac{3}{15}=\frac12\cdot\frac15=\frac{1}{10}\)
=>\(x=\frac{1}{10}+\frac{3}{10}=\frac{4}{10}=\frac25\)
d: \(\frac{5}{14}-x=-\frac{17}{36}:\frac{51}{18}\)
=>\(\frac{5}{14}-x=-\frac{17}{36}\cdot\frac{18}{51}=-\frac{17}{51}\cdot\frac{18}{36}\)
=>\(\frac{5}{14}-x=-\frac13\cdot\frac12=-\frac16\)
=>\(x=\frac{5}{14}+\frac16=\frac{15}{42}+\frac{7}{42}=\frac{22}{42}=\frac{11}{21}\)
e: \(-\frac34x+\frac14\left(x-1\right)=-\frac{12}{5}\)
=>\(-\frac34x+\frac14x-\frac14=-\frac{12}{5}\)
=>\(-\frac24x=-\frac{12}{5}+\frac14=-\frac{48}{20}+\frac{5}{20}=-\frac{43}{20}\)
=>\(\frac{x}{2}=\frac{43}{20}\)
=>\(x=\frac{43}{20}\cdot2=\frac{43}{10}\)
f: \(\left(2x-\frac49\right)\left(3-11x\right)=0\)
=>\(\left[\begin{array}{l}2x-\frac49=0\\ 3-11x=0\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=\frac49\\ 11x=3\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac49:2=\frac29\\ x=\frac{3}{11}\end{array}\right.\)