Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng tập hợp \(S\) là:
\(S=\left\{5+6+7+8+9\right\}\\ S=35\)

Có \(A_8^5=6720\) số bất kì (kể cả bắt đầu bằng 0)
Do vai trò của các chữ số là như nhau, nên ở mỗi vị trí, mỗi chữ số xuất hiện: \(67220:5=1344\) lần
Ta chọn 1 số làm đại diện tính toán, ví dụ số 3, do số 3 xuất hiện ở các hàng chục ngàn, ngàn, trăm, chục, đơn vị mỗi hàng đều 1344 lần nên tổng giá trị của số 3 là:
\(1344.\left(3.10000+3.1000+3.100+3.10+3.1\right)=1344.11111.3\)
Do vai trò các chữ số là giống nhau nên tổng các chữ số là:
\(S_1=1344.11111.\left(0+3+4+5+6+7+8+9\right)\)
Bây giờ ta lập các số có số 0 đứng đầu, nó đồng nghĩa với việc lập số có 4 chữ số từ các chữ số 3,4,5,6,7,8
Số số lập được là: \(A_7^4=840\) số
Do vai trò các chữ số như nhau nên mỗi vị trí mỗi chữ số xuất hiện \(840:4=210\) lần
Tương tự như trên, ta có tổng trong trường hợp này là:
\(S_2=210.1111.\left(3+4+5+6+7+8+9\right)\)
Giờ lấy \(S_1-S_2\) là được

Một số có 6 chữ số đôi một khác nhau được tạo ra từ sáu chữ số 1, 2, 3, 4, 5, 6 là một hoán vị của sáu chữ số này.
Vậy số các số phải tìm là: \({P_6} = 6! = 720\)( số )

Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)

Số bất kì: \(6!-5!\) số
Xếp 0 và 5 cạnh nhau: 2 cách
Hoán vị bộ 05 với 4 chữ số còn lại: \(5!\) cách
Hoán vị bộ 05 với 4 chữ số còn lại sao cho 0 đứng đầu: \(4!\) cách
\(\Rightarrow2.5!-4!\) cách xếp sao cho 0 và 5 cạnh nhau
\(\Rightarrow6!-5!-\left(2.5!-4!\right)\) cách xếp thỏa mãn

a, Số các số tự nhiên gồm 8 chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là: \({P_8} = 8! = 40320\)( số )
b, Số các số tự nhiên gồm 6 chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là: \(P_8^6 = 20160\)( số )

a) Việc lập số chẵn gồm ba chữ số là thực hiện 3 hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục, chọn chữ số hàng trăm.
chọn chữ số hàng đơn vị: Có 3 cách chọn (số 2, 4, 6).
chọn chữ số hàng chục: Có 7 cách chọn.
chọn chữ số hàng trăm: Có 7 cách chọn.
Theo quy tắc nhân, số số chẵn lập được là: 3.7.7=147 (số).
b) Việc lập số chẵn gồm ba chữ số đôi một khác nhau là thực hiện 3 hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục, chọn chữ số hàng trăm.
chọn chữ số hàng đơn vị: Có 3 cách chọn (số 2, 4, 6).
chọn chữ số hàng chục: Có 6 cách chọn.
chọn chữ số hàng trăm: Có 5 cách chọn.
Theo quy tắc nhân, số số chẵn lập được là: 3.6.5=90 (số).

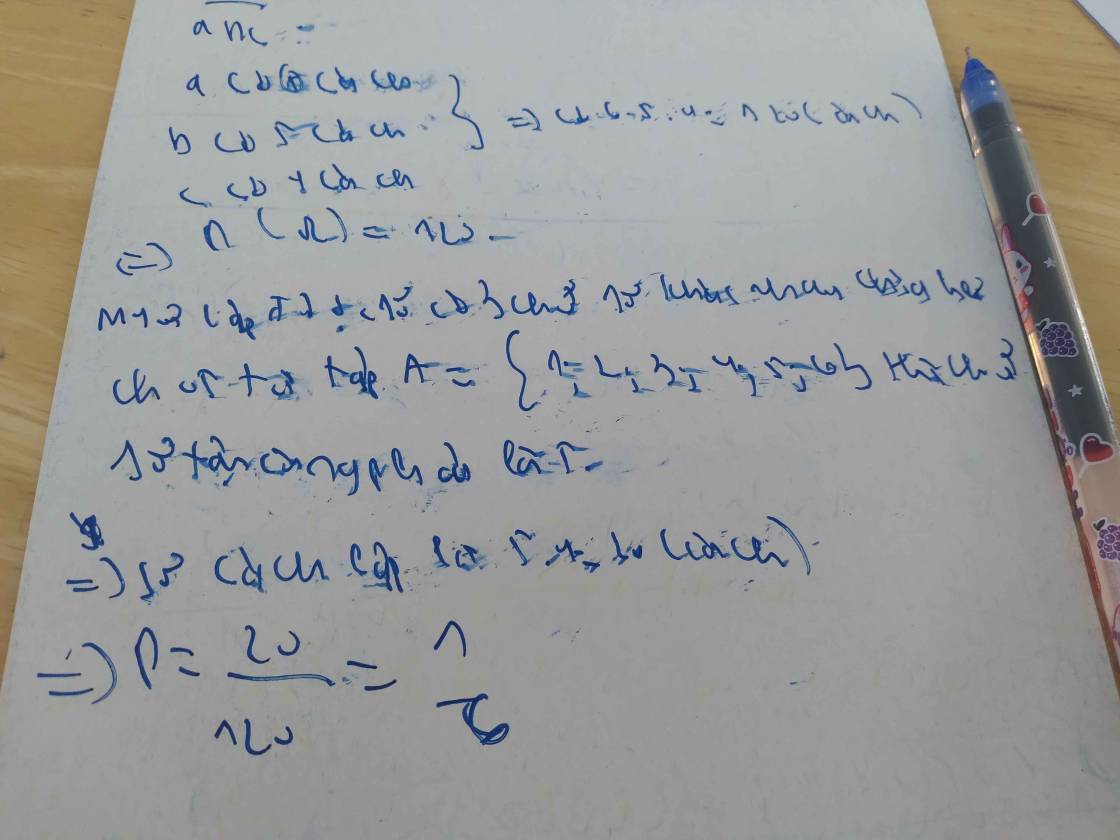
Lời giải:
Gọi các số thỏa mãn có dạng là $\overline{a_1a_2a_3a_4a_5}$
$a_1$ có 6 cách chọn
$a_2$ có 5 cách chọn
$a_3$ có 4 cách chọn
$a_4$ có 3 cách chọn
$a_5$ có 2 cách chọn
$\Rightarrow \overline{a_1a_2a_3a_4a_5}$ có $2.3.4.5.6=720$ cách chọn.
Trong 720 số được tạo ra, mỗi chữ số$1,3,4,5,7,8$, ở mỗi hàng xuất hiện $\frac{720}{6}=120$ lần.
Suy ra tổng các số được tạo là:
$120(1+3+4+5+7+8)(10^4+10^3+10^2+10^1+1)=37332960$