NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
9 tháng 4 2017
a) Ta có:
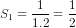
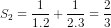
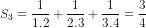
b) Từ câu a) ta dự đoán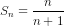 
(1), với mọi n ε N* .
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n = 1, vế trái là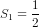 
, vế phải bằng 
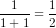. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là
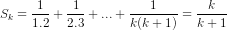
Ta phải chứng minh nó cũng đúng khi n = k + 1, nh=ghĩa là phải chứng minh
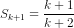
Ta có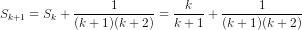 
= 
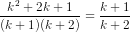
tức là đẳng thức (1) cũng đúng với n = k + 1.
Vậy điều cần chứng minh đúng với mọi n.
BT
24 tháng 5 2017
a) \(u_n=u_1.q^{n-1}=u_1.2^{n-1}\)
\(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}=\dfrac{u_1\left(1-2^n\right)}{1-2}=u_1\left(2^n-1\right)\);
\(\dfrac{S_n}{u_n}=\dfrac{u_1\left(2^n-1\right)}{u_1.2^{n-1}}=\dfrac{2^n-1}{2^{n-1}}=2-\dfrac{1}{2^{n-1}}=\dfrac{63}{32}\)
Vì vậy \(\dfrac{1}{2^{n-1}}=\dfrac{1}{32}\) \(\Leftrightarrow\dfrac{1}{2^{n-1}}=\dfrac{1}{2^5}\)\(\Leftrightarrow n-1=5\Leftrightarrow n=6\).
b)
\(u_n=2.q^{n-1}=\dfrac{1}{8}\)\(\Rightarrow q^{n-1}=\dfrac{1}{16}\)
\(S_n=\dfrac{2\left(1-q^n\right)}{1-q}=\dfrac{2\left(1-q.q^{n-1}\right)}{1-q}=\dfrac{2\left(1-\dfrac{1}{16}q\right)}{1-q}=\dfrac{31}{8}\);
Suy ra \(q=-1\).
BT
23 tháng 5 2017
a)
\(S_1=\dfrac{1}{1.5}=\dfrac{1}{5}\)
\(S_2=\dfrac{1}{1.5}+\dfrac{1}{5.9}=\dfrac{1}{4}\left(\dfrac{1}{1}-\dfrac{1}{5}\right)+\dfrac{1}{4}\left(\dfrac{1}{5}-\dfrac{1}{9}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}\right)=\dfrac{1}{4}\left(1-\dfrac{1}{9}\right)=\dfrac{2}{9}\).
\(S_3=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{13}\right)=\dfrac{3}{13}\).
\(S_4=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}+\dfrac{1}{13.17}\)\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{17}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{17}\right)=\dfrac{4}{17}\).
b) Dự đoán công thức : \(S_n=\dfrac{1}{4}\left(1-\dfrac{1}{4n+1}\right)\).
Chứng minh bằng quay nạp:
Với \(n=1\): \(S_1=\dfrac{1}{1.5}=\dfrac{1}{5}\).
Vậy giả thiết quy nạp đúng với n = 1.
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(S_k=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)\).
Ta sẽ chứng minh nó đúng với \(n=k+1\): \(S_{k+1}=\dfrac{1}{4}\left(1-\dfrac{1}{4\left(k+1\right)+1}\right)\)
Thật vậy:
\(S_{k+1}=S_k+\dfrac{1}{\left[4\left(k+1\right)-3\right].\left[4\left(k+1\right)+1\right]}\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)+\dfrac{1}{4}\left(\dfrac{1}{4\left(k+1\right)-3}-\dfrac{1}{4\left(k+1\right)+1}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)+\dfrac{1}{4}\left(\dfrac{1}{4k+1}-\dfrac{1}{4\left(k+1\right)+1}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4\left(k+1\right)+1}\right)\).
Vậy điều cần chứng minh đúng với mọi n.
SG
2
MH
9 tháng 4 2017
Các số hạng tổng lập thành cấp số nhân lùi vô hạn với u1 = -1 và q = - .
Vậy S = -1 + -
+ ... +
+ ... =
=
=
.
BT
26 tháng 5 2017
Các số hạng lập thành một số nhân với \(u_1=-1\) và \(q=-\dfrac{1}{10}\).
Vậy:
\(S_n=-1+\dfrac{1}{10}-\dfrac{1}{10^2}+...+\dfrac{\left(-1\right)^n}{10^{n-1}}+...=\dfrac{u_1}{1-q_1}\)\(=\dfrac{-1}{1-\left(-\dfrac{1}{10}\right)}=\dfrac{-10}{11}\).
NA
2
NN
20 tháng 4 2016
Xét cấp số cộng (U\(_n\)) có u\(_1\)=105 và công sai d =5 ta đươc:
995=u\(_n\)=u\(_1\)+(n-1)d =105+5(n-1)\(\Leftrightarrow\)n=179
s=s\(_{179}\)=\(\frac{179}{2}\)(u\(_1\)+u\(_{179}\))=\(\frac{179}{2}\)(105+995)=98450
20 tháng 4 2016
Ta có : \(a_1=105;a_2=110\Rightarrow d=5;a_n=995\)
mà \(a_n=a_1+\left(n-1\right)d\Rightarrow995=105+\left(n-1\right)5\)
\(\Rightarrow S=\frac{n\left(a_1+a_n\right)}{2}=98450\)
Ta có : \(S=3\left(1+11+111+...+11...1\right)\) (n chữ số 1)
\(=3\left(\frac{10-1}{9}+\frac{10^2-1}{9}+....\frac{10^n-1}{9}\right)=\frac{3}{9}\left(10+10^2+....+10^n-n\right)\)
\(=\frac{1}{3}\left(10.\frac{10^n-1}{10-1}-n\right)=\frac{1}{27}\left(10^{n+1}-10-9n\right)\)