K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TQ
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 11 2019
Bạn xem lại đề bài, nhìn biểu thức thì số hạng cao nhất chỉ đến mũ 4, không thể có số hạng chứa \(x^5\) được, nếu thích làm cụ thể thì cũng tốn thời gian thôi:
\(\left(1-2x-3x^2\right)^2=\sum\limits^2_{k=0}C_2^k\left(-2x-3x^2\right)^k=\sum\limits^2_{k=0}\sum\limits^k_{i=0}C_2^kC_k^i\left(-2x\right)^i\left(-3x^2\right)^{k-i}\)
\(=\sum\limits^2_{k=0}\sum\limits^k_{i=0}C_2^kC_k^i\left(-2\right)^i\cdot\left(-3\right)^{k-i}.x^{2k-i}\)
Số hạng chứa \(x^5\) có: \(\left\{{}\begin{matrix}0\le k\le2\\0\le i\le k\\2k-i=5\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\) Ko tồn tại i; k thỏa mãn
10 tháng 11 2023
a: \(P=-3x^3+5x\)
\(=x\cdot\left(-3x^2\right)+x\cdot5\)
\(=x\left(-3x^2+5\right)\)
b: \(Q=\left(2x-1\right)+\left(x-2\right)\left(2x-1\right)\)
\(=\left(2x-1\right)\left(1+x-2\right)\)
\(=\left(2x-1\right)\left(x-1\right)\)
c: \(R=4-16x^2\)
\(=4\cdot1-4\cdot4x^2\)
\(=4\left(1-4x^2\right)\)
\(=4\left(1-2x\right)\left(1+2x\right)\)
d: \(S=36-4x^2\)
\(=4\cdot9-4\cdot x^2\)
\(=4\left(9-x^2\right)\)
\(=4\left(3-x\right)\left(3+x\right)\)
e: \(T=8x^3-1\)
\(=\left(2x\right)^3-1^3\)
\(=\left(2x-1\right)\left(4x^2+2x+1\right)\)
f: \(Q=8-x^3\)
\(=2^3-x^3\)
\(=\left(2-x\right)\left(4+2x+x^2\right)\)
g: \(N=64-x^3\)
\(=4^3-x^3\)
\(=\left(4-x\right)\left(16+4x+x^2\right)\)
31 tháng 8 2023
a: \(y'=\left(x^2\right)'+\left(3x\right)'-\left(6x^6\right)'+\left(\dfrac{2x-3}{x-1}\right)'\)
\(=2x+3-6\cdot6x^5+\dfrac{\left(2x-3\right)'\left(x-1\right)-\left(2x-3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{2\left(x-1\right)-2x+3}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{1}{\left(x-1\right)^2}\)
b: \(\left(\sqrt{2x^2-3x+1}\right)'=\dfrac{\left(2x^2-3x+1\right)'}{2\sqrt{2x^2-3x+1}}\)
\(=\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(y'=3\cdot2x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(=6x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
c: \(\left(\sqrt{4x^2-3x+1}\right)'=\dfrac{\left(4x^2-3x+1\right)'}{2\sqrt{4x^2-3x+1}}\)
\(=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)
\(y'=\left(\sqrt{4x^2-3x+1}\right)'-4'=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2020
\(A=\lim\limits_{x\rightarrow2}\frac{\left(x-2\right)\left(2x-1\right)}{x-2}=\lim\limits_{x\rightarrow2}\left(2x-1\right)=3\)
\(B=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2-2x+3\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x^2-2x+3}{x+1}=\frac{1-2+3}{1+1}=1\)
\(C=\lim\limits_{x\rightarrow2}\frac{x^2+2x}{x^2+4x+4}=\frac{4+4}{4+8+4}=\frac{1}{2}\)
\(D=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2-1\right)}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow1}\frac{x^2-1}{x-2}=\frac{0}{-1}=0\)
\(E=\lim\limits_{x\rightarrow1}\frac{x^3-5x^2+3x+9}{x^4-8x^4-9}=\frac{1-5+3+9}{1-8-9}=-\frac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2020
\(F=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x-1\right)\left(x^2+1\right)}{\left(x+1\right)\left(x^2-3x+3\right)}=\lim\limits_{x\rightarrow-1}\frac{\left(x-1\right)\left(x^2+1\right)}{x^2-3x+3}=\frac{-2.2}{1+3+3}=-\frac{2}{5}\)
\(G=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(2x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x+3}{2x+1}=\frac{4}{3}\)
\(H=\lim\limits_{x\rightarrow-2}\frac{\left(x+2\right)\left(x-1\right)^2}{\left(2-x\right)\left(x+2\right)}=\lim\limits_{x\rightarrow-2}\frac{\left(x-1\right)^2}{2-x}=\frac{9}{4}\)
\(I=\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+1}{x^2-1}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4}{2x}=\frac{24-25}{2}=-\frac{1}{2}\)
\(K=\lim\limits_{x\rightarrow1}\frac{x^m-1}{x^n-1}=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)
13 tháng 3 2023
\(=\lim\limits_{x->1}\dfrac{\left(x-1\right)\left(x-2\right)}{\sqrt{3x+1}-2-2\left(\sqrt[3]{2x-1}-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x-2\right)}{\dfrac{3x+1-4}{\sqrt{3x+1}+2}-2\cdot\dfrac{2x-1-1}{\sqrt[3]{\left(2x-1\right)^2}+\sqrt[3]{2x-1}+1}}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-2\right)}{\dfrac{3}{\sqrt{3x+1}+2}-\dfrac{4}{\sqrt[3]{\left(2x-1\right)^2}+\sqrt[3]{2x-1}+1}}\)
\(=\dfrac{1-2}{\dfrac{3}{\sqrt{3+1}+2}-\dfrac{4}{\sqrt[3]{\left(2\cdot1-1\right)^2}+\sqrt[3]{2\cdot1-1}+1}}\)
\(=-1:\dfrac{-7}{12}=\dfrac{12}{7}\)
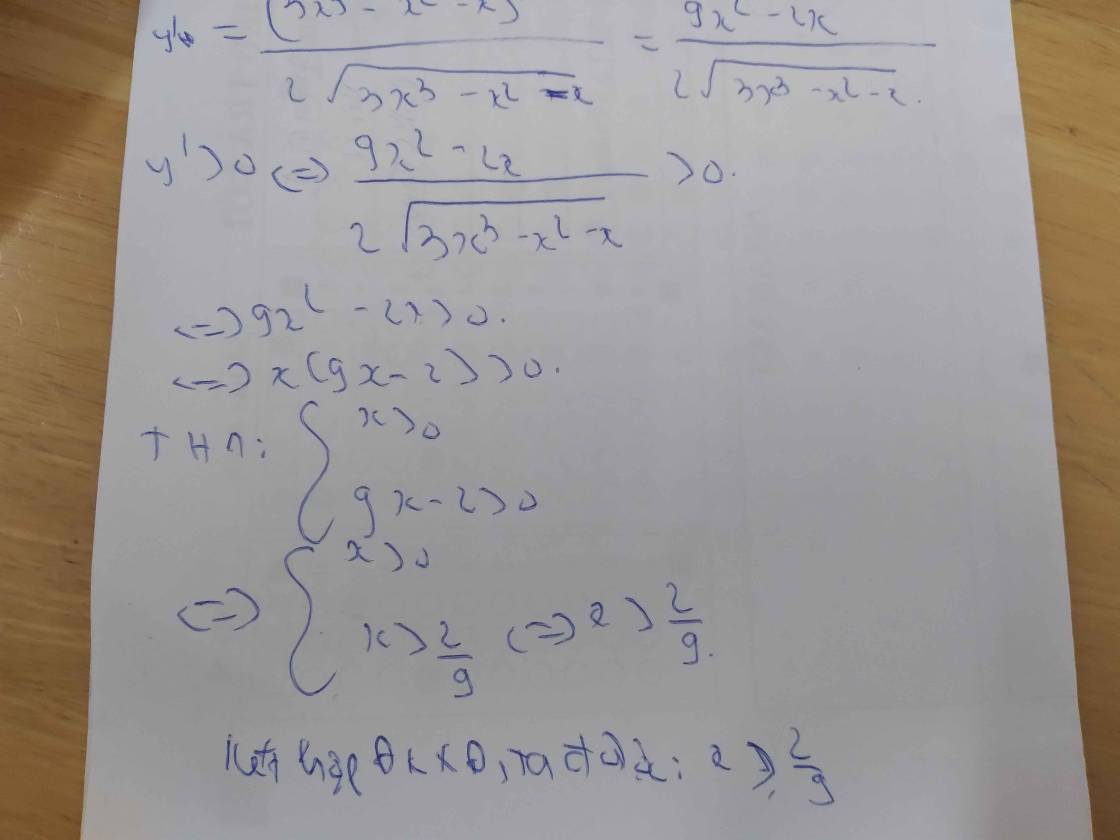
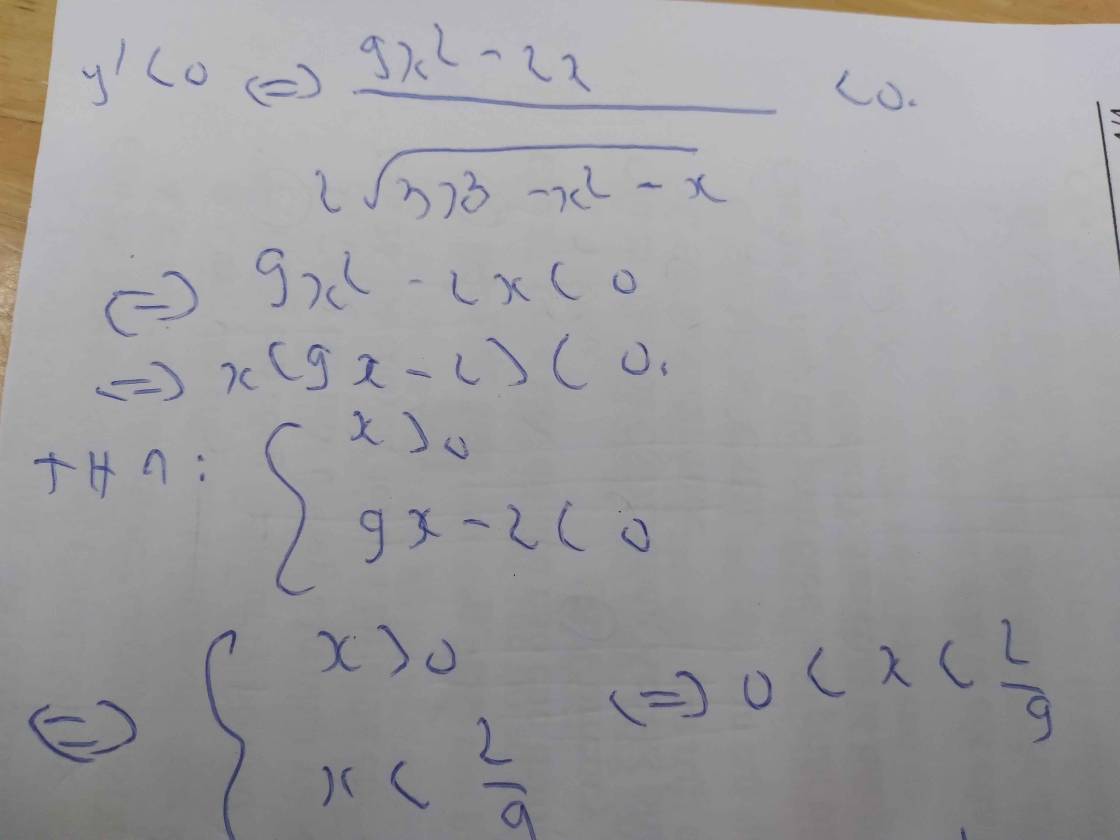
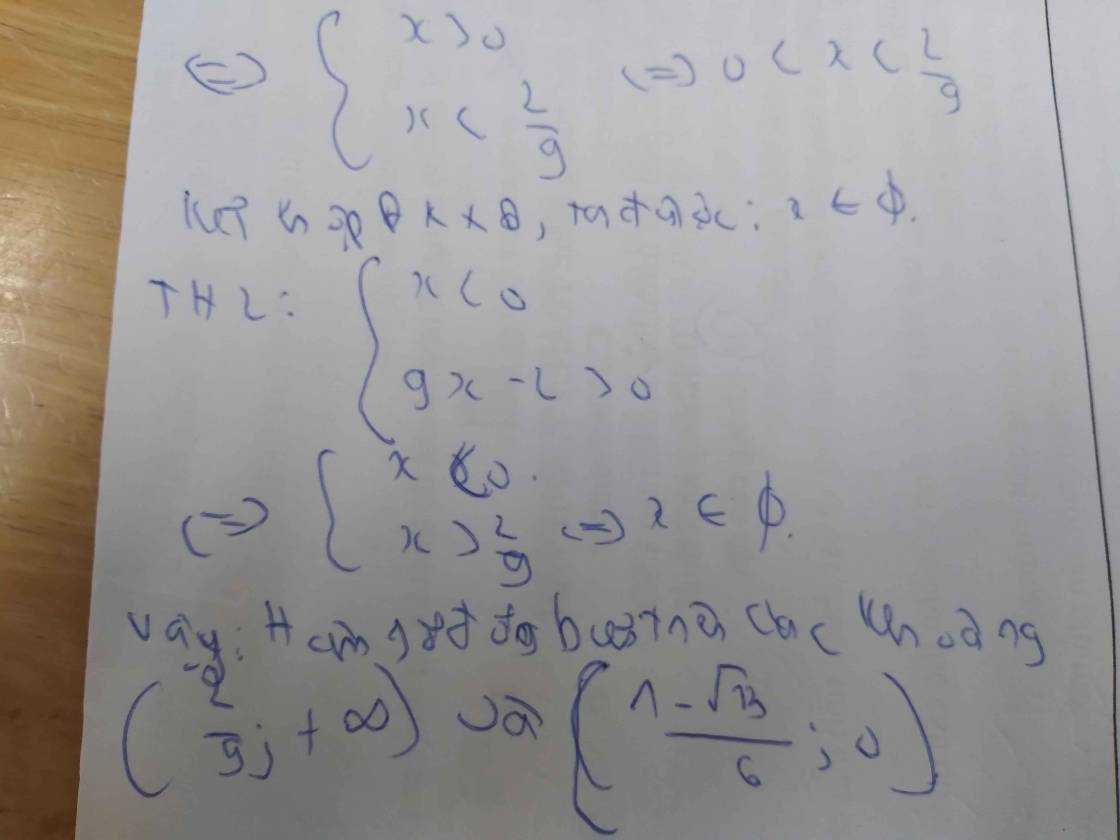
Xét khai triển:
\(\left(1+x\right)^n=1+x+x^2+...+x^n\)
Đạo hàm 2 vế:
\(\Rightarrow n\left(x+1\right)^{n-1}=1+2x+3x^2+...+nx^{n-1}\)
Vậy \(S=n\left(x+1\right)^{n-1}\)