TQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
1.
\(y'=12x+\dfrac{4}{x^2}\)
2.
\(y'=\dfrac{3}{\left(-x+1\right)^2}\)
3.
\(y'=\dfrac{2x-3}{2\sqrt{x^2-3x+4}}\)
4.
\(y=\dfrac{x^3+3x^2-x-3}{x-4}\)
\(y'=\dfrac{\left(3x^2+6x-1\right)\left(x-4\right)-\left(x^3+3x^2-x-3\right)}{\left(x-4\right)^2}=\dfrac{2x^3-9x^2-24x+7}{\left(x-4\right)^2}\)
5.
\(y'=-\dfrac{4x-3}{\left(2x^2-3x+5\right)^2}\)
6.
\(y'=\sqrt{x^2-1}+\dfrac{x\left(x+1\right)}{\sqrt{x^2-1}}\)
PT
1
CM
6 tháng 8 2018
Chọn B.
Ta có: y = (2x – 1)(3x + 2) = (2x2 – x)(3x + 2)
y’ = [(2x2 – x)(3x + 2)]’ = (2x2 – x)’(3x + 2) + (3x + 2)’.(2x2 – x)
= (4x – 1)(3x + 2) + 3(2x2 – x) = 18x2 + 2x – 2.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2020
\(\left(2x-1\right)^6\left(3x^2+1\right)^5=\sum\limits^6_{k=0}C_6^k\left(2x\right)^k\left(-1\right)^{6-k}\sum\limits^5_{i=0}C_5^i\left(3x^2\right)^i\)
\(=\sum\limits^6_{k=0}\sum\limits^5_{i=0}C_6^k.C_5^i.\left(-1\right)^{6-k}.2^k.3^i.x^{k+2i}\)
Số hạng chứa \(x^4\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le k\le6\\0\le i\le5\\k+2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;4\right);\left(1;2\right);\left(2;0\right)\)
Hệ số:
\(C_6^4.C_5^0\left(-1\right)^4.2^4.3^0+C_6^2C_5^1\left(-1\right)^2.2^2.3^1+C_6^0.C_5^2.\left(-1\right)^0.2^0.3^2=...\)
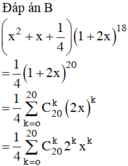
Bạn xem lại đề bài, nhìn biểu thức thì số hạng cao nhất chỉ đến mũ 4, không thể có số hạng chứa \(x^5\) được, nếu thích làm cụ thể thì cũng tốn thời gian thôi:
\(\left(1-2x-3x^2\right)^2=\sum\limits^2_{k=0}C_2^k\left(-2x-3x^2\right)^k=\sum\limits^2_{k=0}\sum\limits^k_{i=0}C_2^kC_k^i\left(-2x\right)^i\left(-3x^2\right)^{k-i}\)
\(=\sum\limits^2_{k=0}\sum\limits^k_{i=0}C_2^kC_k^i\left(-2\right)^i\cdot\left(-3\right)^{k-i}.x^{2k-i}\)
Số hạng chứa \(x^5\) có: \(\left\{{}\begin{matrix}0\le k\le2\\0\le i\le k\\2k-i=5\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\) Ko tồn tại i; k thỏa mãn