
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thêm nữa câu a) Tính: M(x) + N(x)+ P(x)
B) Tính M(x) - N (x) - P(x)
ok rồi giúp mình với nha

Bài 8:
a: \(\left(\dfrac{2}{5}+\dfrac{3}{4}\right)^2=\left(\dfrac{8+15}{20}\right)^2=\left(\dfrac{23}{20}\right)^2=\dfrac{529}{400}\)
b: \(\left(\dfrac{5}{4}-\dfrac{1}{6}\right)^2=\left(\dfrac{15}{12}-\dfrac{2}{12}\right)^2=\left(\dfrac{13}{12}\right)^2=\dfrac{169}{144}\)

a,(\(6x-5x^2-15+2x^3:\left(2x-5\right)\)
\(\left(2x^3-5x^2+6x-15\right):\left(2x-5\right)\)
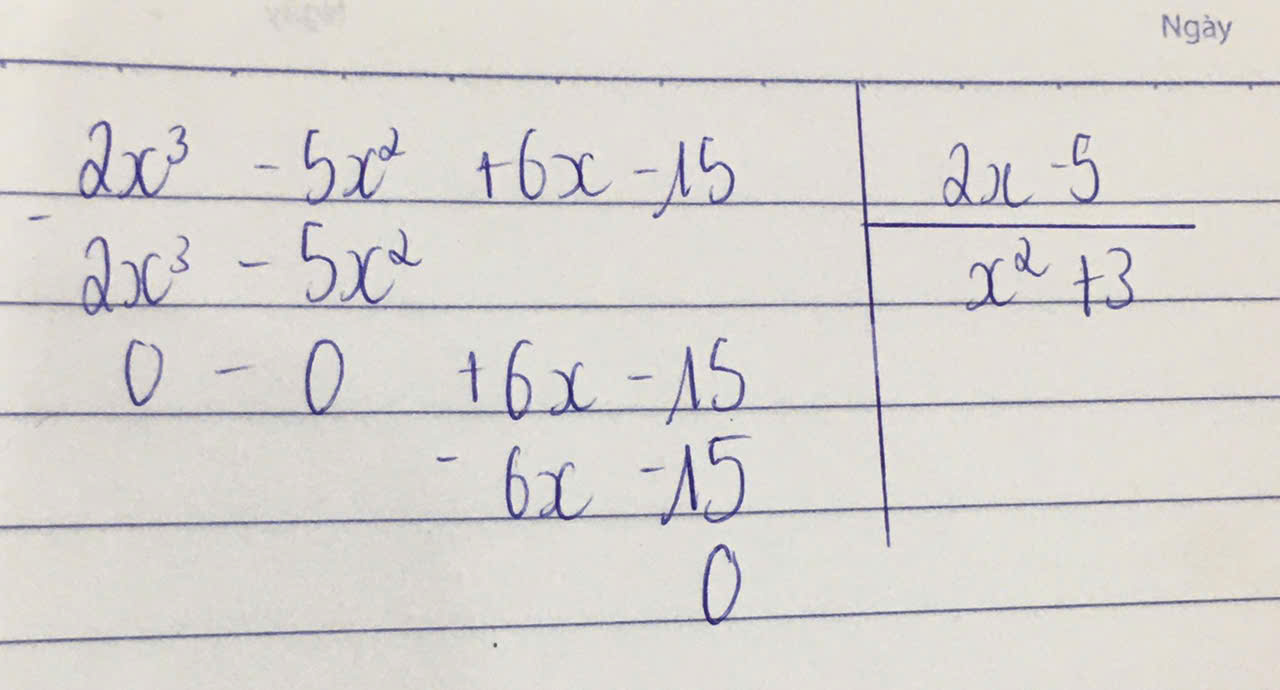

a,\(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2\)
\(=\left(\dfrac{13}{14}\right)^2\)
\(=\dfrac{169}{196}\)
b,\(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2\)
\(=\left(\dfrac{-1}{12}\right)^2\)
\(=\dfrac{1}{144}\)
c,\(\dfrac{5^4.20^4}{25^5.4^5}\)
\(=\dfrac{100^4}{100^5}\)
\(=\dfrac{1}{100}\)
d,\(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4\)
\(=\left(\dfrac{-10}{3}\right)^4.\left(\dfrac{-6}{5}\right)^4.\left(\dfrac{-10}{3}\right)\)
\(=\left(\dfrac{\left(-10\right)}{3}.\dfrac{\left(-6\right)}{5}\right)^4.\left(\dfrac{-10}{3}\right)\)
\(=4^4.\left(\dfrac{-10}{3}\right)\)
\(=256.\left(\dfrac{-10}{3}\right)\)
\(=\dfrac{-2560}{3}\)
=15\(^3\)
Mình làm bài tổng quát nha để bạn hiểu sau rồi bạn thay vào .
Đặt \(S_1=1+2+...+n\)
\(\Rightarrow S_1=\frac{n\left(n+1\right)}{2}\)
Đặt \(S_2=1^2+2^2+...+n^2\)
Ta có:
\(2^3=\left(1+1\right)^3=1^3+3.1^2+3.1+1\)
\(3^3=\left(2+1\right)^3=2^3+3.2^2+3.2+1\)
..................................................................................
\(\left(n+1\right)^3=n^3+3n^2+3n+1\)
Cộng từng vế n thẳng đẳng thức trên ta được :
\(\left(n+1\right)^3=1^3+3.\left(1^2+2^2+...+n^2\right)+3.\left(1+2+3+...+n\right)+n\)
\(\Rightarrow\left(n+1\right)^3=1^3+3.\left(1^2+2^2+...+n^2\right)+\frac{3n\left(n+1\right)}{2}+n\)
\(\Rightarrow3.\left(1^2+2^2+...+n^2\right)=\left(n+1\right)^3-\frac{3n\left(n+1\right)}{2}-\left(n+1\right)\)
Hay \(3S_2=\left(n+1\right)\left[\left(n+1\right)^2-\frac{3n}{2}-1\right]\)
\(\Rightarrow3S_2=\left(n+1\right)\left(n^2+\frac{n}{2}\right)\)
\(\Rightarrow3S_2=\frac{1}{2}n\left(n+1\right)\left(2n+1\right)\)
\(\Rightarrow S_2=\frac{1}{6}n\left(n+1\right)\left(2n+1\right)\)
Đặt \(S_3=1^3+2^3+...+n^3\)
Ta có:
\(\left(1+1\right)^4=1^4+4.1^3+6.1^2+4.1+1\)
\(\left(2+1\right)^4=2^4+4.2^3+6.2^2+4.2+1\)
........................................................................................
\(\left(n+1\right)^4=n^4+4n^3+6n^2+4n+1\)
Cộng từng vế n đẳng thức trên ta được :
\(\left(n+1\right)^4=1^4+4.\left(1^3+2^3+...+n^3\right)+6.\left(1^2+2^2+...+n^2\right)+4.\left(1+2+...+n\right)+n\)
\(\Rightarrow\left(n+1\right)^4=1+4S_3+6S_2+4S_1+n\)
Đã chứng minh \(S_1=\frac{n\left(n+1\right)}{2}\)
\(S_2=\frac{1}{6}n\left(n+1\right)\left(2n+1\right)\)
Từ đó tính được :
\(S_3=\frac{n^2\left(n+1\right)^2}{4}\)
đó là công thức giờ chỉ vệc thay vào
\(1^3+2^3+3^3+4^3+5^3=\frac{5^2\left(5+1\right)^2}{4}=225\)