Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

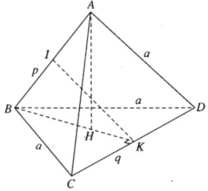
Gọi I và K lần lượt là trung điểm của AB và CD (h.3.80), ta có IK là đoạn vuông góc chung của AB và CD và độ dài đoạn IK là khoảng cách cần tìm:
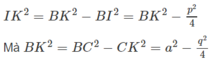
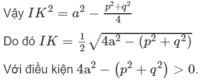

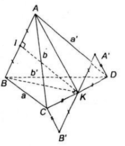
Gọi I, K lần lượt là trung điểm của cạnh AB và CD
Qua K kẻ đường thẳng d // AB, trên d lấy A', B' sao cho K là trung điểm của A'B' và
KA' = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( giả thiết)
KB’= KA’( cách dựng)
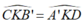 ( hai góc đối đỉnh )
( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K có IB= KB’ và IB // KB’ ( cách dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
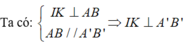
Lại có:IK ⊥ CK
=> IK ⊥ (CKB') (**)
Từ (*) và (**) suy ra BB' ⊥ (CKB') ; AA' ⊥ (CKB')
⇒ BB' ⊥ B'C; AA' ⊥ A'D
* Xét hai tam giác vuông BCB’ và ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* Chứng minh tương tự, AC = BD

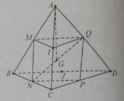
Ta có N là trung điểm của BC
Suy ra A B → + A C → = 2 A N →
Lại có: A D → = 2 A Q → (Q là trung điểm của AD)
Do đó A B → + A C → + A D → = 2 A N → + 2 A Q → = 2 A N → + A Q → (1)
Tạ lại có G là trọng tâm của tứ diện ABCD nên G là trung điểm của NQ (tính chất trọng tâm của tứ diện) ⇒ A N → + A Q → = 2 A G → (2)
Từ (1) và (2) suy ra A B → + A C → + A D → = 4 A G → .
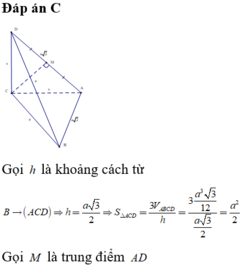
Đáp án A

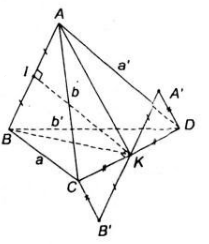

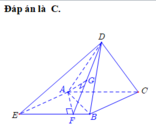
Gọi I và K lần lượt là trung điểm của AB và CD , ta có IK là đoạn vuông góc chung của AB và CD và độ dài đoạn IK là khoảng cách cần tìm :