Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử tam giác ABC cân tại C, AC = BC = a, C = α
Diện tích tam giác là:
S = 1 2 a b . sin C = 1 2 a . a . sin α = 1 2 a 2 sin α
ĐÁP ÁN B

Tham khảo:
Kí hiệu các điểm A, B, C như hình dưới

Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(BC = 3,2;\widehat A = {180^o} - ({48^o} + {105^o}) = {27^o}\)
Áp dụng định lí sin, ta có:
\(\frac{b}{{\sin B}} = \frac{a}{{\sin A}} \Rightarrow AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{3,2.\sin {{48}^o}}}{{\sin {{27}^o}}} \approx 5,24(m)\)
Áp dụng công thức \(S = \frac{1}{2}ab\sin C\) ta có:
\(S = \frac{1}{2}.3,2.5,24\sin {105^o} \approx 8,1({m^2})\)

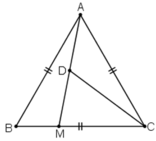
a) Do tam giác ABC là tam giác đều nên 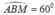 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
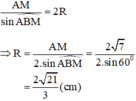
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
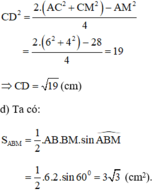

\(AM=AB+BM=13\left(cm\right)\)
\(AN=AC+CN=16\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\Rightarrow sinA=\dfrac{2S_{ABC}}{AB.AC}=\dfrac{3}{4}\)
\(\Rightarrow S_{AMN}=\dfrac{1}{2}AM.AN.sinA=\dfrac{1}{2}.13.16.\dfrac{3}{4}=...\)

a: Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-75^0-45^0=60^0\)
Xét ΔABC có
\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)
=>\(\dfrac{AB}{sin45}=\dfrac{50}{sin60}\)
=>\(AB\simeq40,82\)
b: \(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot40,82\cdot50\cdot sin75\simeq985,73\)
c: Độ dài đường cao xuất phát từ A là:
\(2\cdot\dfrac{985.73}{50}=39,4292\left(\right)\)

Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=7\)
Diện tích:
\(S_{ABC}=\dfrac{1}{2}ac.sinB=10\sqrt{3}\)


Kí hiệu các điểm A, B, C như hình trên.
Từ giả thiết ta có: \(AB = AC = 90,\widehat A = {35^o}\)
Áp dụng công thức \(S = \frac{1}{2}bc\sin A\), ta có: \(S = \frac{1}{2}.90.90.\sin {35^o} \approx 2323\;(c{m^2})\)