Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
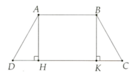

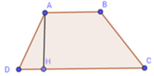
SABCD = ( A B + C D ) A H 2
=> AH = 2 S A B C D A B + C D = 2.60 10 + 5 = 8 (cm)
Đáp án cần chọn là: A

Tương tự 1B. Tính được số đo của A ^ = 135 0 , B ^ = 90 0 , C ^ = 90 0 , D ^ = 45 0 , từ đó suy ra ABCD là hình thang vuông ⇒ B C ⊥ D C . Vận dụng nhận xét hình thang ABCH (AB//CH) có hai cạnh bên song song thì hai cạnh đáy bằng nhau, để tính được CH = 3cm, từ đó suy ra DH = 1cm.
Chứng minh được DAHD vuông cân tại H Þ AH = 1cm
Þ diện tích hình thang ABCD là 3,5cm2

Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2