bài 1 cho hình thang ABCD (AB // CD và AB < CD ) trên đg AD lấy AE = EM = MP = PD .Trên đg BC lấy BF = FN = NQ = QC .1) C/m M, N lần lượt là trung điểm của AD và BC.2) tứ giác EFQP là hình gì ?3) tính MN ,EF ,PQ biết AB = 8 cm và CD = 12 cm4) kẻ AH vuông góc tại H và AH = 10 cm . tính \(S_{ABCD}\)bài 2 cho tam giác ABCD . Trên cạnh AB lấy AD = DE = EB . Từ D, E kẻ các đg thẳng cùng song song với BC cắt cạnh AC lần lượt tại...
Đọc tiếp
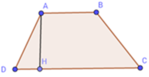
bài 1 cho hình thang ABCD (AB // CD và AB < CD ) trên đg AD lấy AE = EM = MP = PD .Trên đg BC lấy BF = FN = NQ = QC .
1) C/m M, N lần lượt là trung điểm của AD và BC.
2) tứ giác EFQP là hình gì ?
3) tính MN ,EF ,PQ biết AB = 8 cm và CD = 12 cm
4) kẻ AH vuông góc tại H và AH = 10 cm . tính \(S_{ABCD}\)
bài 2 cho tam giác ABCD . Trên cạnh AB lấy AD = DE = EB . Từ D, E kẻ các đg thẳng cùng song song với BC cắt cạnh AC lần lượt tại M, N . C/m rằng : 1) M là trung điểm của AN.
2) AM = MN = NC .
3) 2EN = DM + BC .
4)\(S_{ABC}=3S_{AMB}\)
bài 3 : cho hình thang ABCD ( AB //CD ) có đg cao AH = 3 cm và AB = 5cm , CD = 8cm gọi E, F , I lần lượt là trung điểm của AD , BC và AC.
1) C/m E ,F ,I thẳng hàng .
2) tính \(S_{ABCD}\)
3) so sánh \(S_{ADC}\) và \(2S_{ABC}\)
bài 4: cho tứ giác ABCD . gọi E, F, I lần lượt là trung điểm AD , BC và AC .1) C/m E, I , F thẳng hàng
2) tính EF≤ AB+CD / 2
3) tứ giác ABCD phải có điều kiện gì thì EF = AB+CD / 2





SABCD = ( A B + C D ) A H 2
=> AH = 2 S A B C D A B + C D = 2.60 10 + 5 = 8 (cm)
Đáp án cần chọn là: A