Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích hình phẳng cần tìm là:
S=2∫−1(x2+1)dx=(x33+x)∣∣2−1=6
b) Diện tích hình phẳng cần tìm là:
S=e∫1e| lnx |dx=e∫1e|lnx|dx+e∫1|lnx|dx=−1∫1elnxdx+e∫1lnxdxS=∫1ee|lnx|dx=∫1ee|lnx|dx+∫1e|lnx|dx=−∫1e1lnxdx+∫1elnxdx
Mặt khác:
∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C
Do đó:
S=−1∫1elnxdx+e∫1lnxdx=1e∫1lnxdx+e∫1xdx=(xlnx−x)∣∣∣1e1+(xlnx−x)∣∣e1=2(1- \(\dfrac{1}{e}\))
Khó quá, làm mà điên não

\(\left(x+1\right)e^x=0\Rightarrow x=-1\)
\(S=\int\limits^0_{-2}\left|\left(x+1\right)e^x\right|dx=-\int\limits^{-1}_{-2}\left(x+1\right)e^xdx+\int\limits^0_{-1}\left(x+1\right)e^xdx\)
\(=\dfrac{2e-2}{e^2}\)

Đáp án D
Phương pháp:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) , trục Ox, đường thẳng
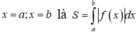
Để tìm đủ cận tích phân ta đi giải phương trình f(x) = 0.
Sử dụng phương pháp tích phân từng phần để tính toán.
Cách giải:

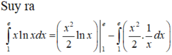
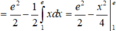
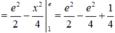
![]()
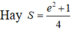

d.
\(\lim\limits_{x\rightarrow\infty}\frac{2x+1}{x+1}=2\Rightarrow y=2\) là TCN của (C)
Diện tích:
\(S=\int\limits^3_1\left(2-\frac{2x+1}{x+1}\right)dx=\int\limits^3_1\frac{1}{x+1}dx=ln\left|x+1\right||^3_1=ln4-ln2=ln2\)
e.
Pt hoành độ giao điểm:
\(2-x^2=x\Leftrightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_{-2}\left(2-x^2-x\right)dx=\left(2x-\frac{1}{3}x^3-\frac{1}{2}x^2\right)|^1_{-2}=\frac{9}{2}\)
a. Pt hoành độ giao điểm: \(\frac{e^x\left(1+x\right)}{1+xe^x}=0\Rightarrow x=-1\)
Diện tích:
\(S=\int\limits^0_{-1}\frac{e^x+xe^x}{1+xe^x}dx\)
Đặt \(1+xe^x=t\Rightarrow\left(e^x+xe^x\right)dx=dt\) ; \(\left\{{}\begin{matrix}x=-1\Rightarrow t=1-\frac{1}{e}\\x=0\Rightarrow t=1\end{matrix}\right.\)
\(S=\int\limits^1_{1-\frac{1}{e}}\frac{dt}{t}=ln\left|t\right||^1_{1-\frac{1}{e}}=-ln\left|\frac{e-1}{e}\right|=ln\left(\frac{e}{e-1}\right)\)
b. Đồ thị \(y=3^x\) ko cắt trục hoành
Diện tích:
\(S=\int\limits^2_03^xdx=\frac{3^x}{ln3}|^2_0=\frac{9}{ln3}-\frac{1}{ln3}=\frac{8}{ln3}\)
c.
Pt hoành độ giao điểm:
\(x^4-4x^2+4=x^2\Leftrightarrow x^4-5x^2+4=0\Rightarrow\left[{}\begin{matrix}x^2=1\\x^2=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_0\left(x^4-4x^2+4-x^2\right)dx=\int\limits^1_0\left(x^4-5x^2+4\right)dx\)
\(=\left(\frac{1}{5}x^5-\frac{5}{3}x^3+4x\right)|^1_0=\frac{38}{15}\)
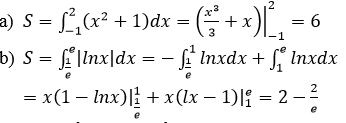
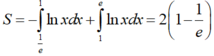
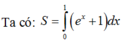
Chọn C
Diện tích hình phẳng được tính bởi