Tính đạo hàm của các hàm số sau: y = x...

K

Khách

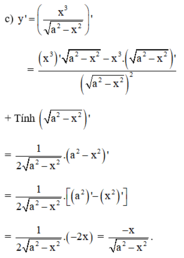
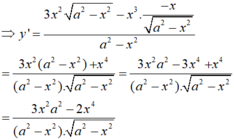
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

22 tháng 7 2018

Tính đạo hàm của các hàm số sau: y = x 3 a 2 - x 2 a là hằng số

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

22 tháng 7 2018

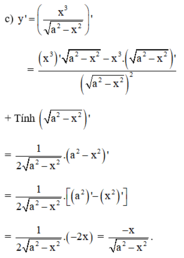
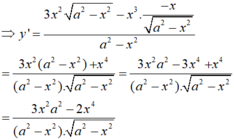
Giải bài 4 trang 163 sgk Đại Số 11 | Để học tốt Toán 11

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

4 tháng 4 2017

Tìm đạo hàm của các hàm số sau :

a) \(y=x^2-x\sqrt{x}+1\)

b) \(y=\sqrt{2-5x-x^2}\)

c) \(y=\dfrac{x^3}{\sqrt{a^2-x^2}}\) (a là hằng số)

d) \(y=\dfrac{1+x}{\sqrt{1-x}}\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

MH

Minh Hải

9 tháng 4 2017

a) y' = 2x - $\left ( \sqrt{x}+x.\frac{1}{2\sqrt{x}} \right )$ = 2x - $\frac{3}{2}\sqrt{x}$ .

b) y' = $\frac{\left ( 2-5x-x^{2} \right )'}{2.\sqrt{2-5x-x^{2}}}$ = $\frac{-5-2x}{2\sqrt{2-5x-x^{2}}}$ .

c) y' = $\frac{\left ( x^{3} \right )'.\sqrt{a^{2}-x^{2}}-x^{3}.\left ( \sqrt{a^{2}-x^{2}} \right )}{a^{2}-x^{2}}$ = $\frac{3x^{2}.\sqrt{a^{2}-x^{2}}-x^{3}.\frac{-2x}{2\sqrt{a^{2}-x^{2}}}}{a^{2}-x^{2}}$ = $\frac{3x^{2}.\sqrt{a^{2}-x^{2}}+\frac{x^{4}}{\sqrt{a^{2}-x^{2}}}}{a^{2}-x^{2}}$ = $\frac{x^{2}\left ( 3a^{2}-2x^{2} \right )}{\left ( a^{2} -x^{2}\right )\sqrt{a^{2}-x^{2}}}$ .

d) y' = $\frac{\left ( 1+x \right )'.\sqrt{1-x}-\left ( 1+x \right ).\left ( \sqrt{1-x} \right )'}{1-x}$ = $\frac{\sqrt{1-x}-\left ( 1+x \right )\frac{-1}{2\sqrt{1-x}}}{1-x}$ = $\frac{2\left ( 1-x \right )+1+x}{2\left ( 1-x \right )\sqrt{1-x}}$ = $\frac{3-x}{2\left ( 1-x \right )\sqrt{1-x}}$ .

SG

Sách Giáo Khoa

11 tháng 4 2017

Tìm đạo hàm của hàm số sau :

\(y=\left(a+\dfrac{b}{x}+\dfrac{c}{x^2}\right)^4\) (a, b, c là các hằng số)

#Hỏi cộng đồng OLM #Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 5 2022

Giải sách bài tập Toán 11 | Giải sbt Toán 11

SG

Sách Giáo Khoa

4 tháng 4 2017

Tìm đạo hàm của các hàm số sau :

a) \(y=\left(x^7-5x^2\right)x^3\)

b) \(y=\left(x^2+1\right)\left(5-3x^2\right)\)

c) \(y=\dfrac{2x}{x^2-1}\)

d) \(y=\dfrac{3-5x}{x^2-x+1}\)

e) \(y=\left(m+\dfrac{n}{x^2}\right)^3\) (m, n là các hằng số)

#Hỏi cộng đồng OLM #Toán lớp 11

1

MH

Minh Hải

9 tháng 4 2017

a) y' = 3.(x⁷- 5x²)².(x⁷- 5x²)' = 3.(x⁷- 5x²)².(7x⁶ - 10x) = 3x.(x⁷- 5x²)²(7x⁵ - 10).

b) y = 5x² - 3x⁴ + 5 - 3x² = -3x⁴ + 2x² + 5, do đó y' = -12x³ + 4x = -4x.(3x² - 1).

c) y' = $\frac{\left ( 2x \right )'.\left ( x^{2}-1 \right )-2x\left ( x^{2}-1 \right )'}{\left ( x^{2}-1 \right )^{2}}$ = $\frac{2.\left ( x^{2}-1 \right )-2x.2x}{\left ( x^{2}-1 \right )^{2}}$ = $\frac{-2\left ( x^{2}+1 \right )}{\left ( x^{2}-1 \right )^{2}}$ .

d) y' = $\frac{\left ( 3-5x \right )\left ( x^{2}-x+1 \right )-\left ( 3-5x \right ).\left ( x^{2}-x+1 \right )'}{\left ( x^{2}-x+1 \right )^{2}}$ = $\frac{-5\left ( x^{2}-x+1 \right )-\left ( 3-5x \right ).\left ( 2x-1 \right )}{\left ( x^{2}-x+1 \right )^{2}}$ = $\frac{5x^{2}-6x-2}{\left ( x^{2}-x+1 \right )^{2}}$ .

e) y' = 3. $\left ( m+\frac{n}{x^{2}} \right )^{2}$ . $\left ( m+\frac{n}{x^{2}} \right )'$ = 3. $\left ( m+\frac{n}{x^{2}} \right )^{2}$ $\left ( -\frac{2n}{x^{3}} \right )$ = - $\frac{6n}{x^{3}}$ . $\left ( m+\frac{n}{x^{2}} \right )^{2}$ .

B

Buddy

17 tháng 8 2023

Tính đạo hàm của các hàm số sau:

a) \(y = {x^2} + 1;\)

b) \(y = kx + c\) (với k, c là các hằng số).

#Hỏi cộng đồng OLM #Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

18 tháng 8 2023

a: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{x^2+1-x_0^2-1}{x-x_0}\)

\(=\lim\limits_{x\rightarrow x0}\dfrac{\left(x-x0\right)\left(x+x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}x+x0=x0+x0=2x0\)

b: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}\)

\(=\lim\limits_{x\rightarrow x0}\dfrac{kx+c-k\cdot x0-c}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{k\left(x-x0\right)}{x-x0}\)

=\(\lim\limits_{x\rightarrow x0}k=k\)

TM

Trần Mai Linh

25 tháng 4 2021

Tìm đạo hàm của hàm số \(y=\dfrac{a^3}{\sqrt{a^2-x^2}}\) (a là hằng số)

Giúp mình với ạ, mình cảm ơnn

#Hỏi cộng đồng OLM #Toán lớp 11

1

HT

Hoàng Tử Hà

26 tháng 4 2021

\(y'=\dfrac{\left(a^3\right)'.\sqrt{a^2-x^2}-\left(\sqrt{a^2-x^2}\right)'.a^3}{a^2-x^2}=\dfrac{-\dfrac{1}{2\sqrt{a^2-x^2}}\left(a^2-x^2\right)'.a^3}{a^2-x^2}\)

\(y'=\dfrac{x.a^3}{\sqrt{a^2-x^2}\left(a^2-x^2\right)}\)

B

Buddy

17 tháng 8 2023

Sử dụng định nghĩa, tìm đạo hàm của các hàm số sau:

a) \(y = k{x^2} + c\) (với k, c là các hằng số);

b) \(y = {x^3}.\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) Với \({x_0}\) bất kì, ta có:

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k{x^2} + c - \left( {kx_0^2 + c} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k\left( {{x^2} - x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k\left( {x - {x_0}} \right)\left( {x + {x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left[ {k\left( {x + {x_0}} \right)} \right] = 2k{x_0}\)

Vậy hàm số \(y = k{x^2} + c\) có đạo hàm là hàm số \(y' = 2kx\)

b) Với \({x_0}\) bất kì, ta có:

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)

Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)

SG

Sách Giáo Khoa

4 tháng 4 2017

Tìm vi phân của các hàm số sau :

a) \(y=\dfrac{\sqrt{x}}{a+b}\) (a, b là các hằng số)

b) \(y=\left(x^2+4x+1\right)\left(x^2-\sqrt{x}\right)\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

QD

Quốc Đạt

4 tháng 4 2017

a) \(dy=d\left(\dfrac{\sqrt{x}}{a+b}\right)=\left(\dfrac{\sqrt{x}}{a+b}\right)dx=\dfrac{1}{2\left(a+b\right)\sqrt{x}}dx\)

b) \(dy=d\left(x^2+4x+1\right)\left(x^2-\sqrt{x}\right)=\left[\left(2x+4\right)\left(x^2-\sqrt{x}\right)+\left(x^2+4x+1\right)\left(2x-\dfrac{1}{2\sqrt{x}}\right)\right]dx\)

SG

Sách Giáo Khoa

4 tháng 4 2017

Tìm đạo hàm của các hàm số sau :

a) \(y=\dfrac{x-1}{5x-2}\)

b) \(y=\dfrac{2x+3}{7-3x}\)

c) \(y=\dfrac{x^2+2x+3}{3-4x}\)

d) \(y=\dfrac{x^2+7x+3}{x^2-3x}\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

MH

Minh Hải

9 tháng 4 2017

a) $y'=\frac{\left ( x-1 \right )'.\left ( 5x-2 \right )-\left ( x-1 \right ).\left ( 5x-2 \right )'}{\left ( 5x-2 \right )^{2}}$ = $\frac{5x-2-\left ( x-1 \right ).5}{\left ( 5x-2 \right )^{2}}$ = $\frac{3}{\left ( 5x-2 \right )^{2}}$ .

b) $y'=\frac{\left ( 2x+3 \right )'.\left ( 7-3x \right )-\left ( 2x+3 \right ).\left ( 7-3x \right )'}{\left ( 7-3x \right )^{2}}$ = $\frac{2\left ( 7-3x \right )-\left ( 2x+3 \right ).\left ( -3 \right )}{\left ( 7-3x \right )^{2}}$ = $\frac{23}{\left ( 7-3x \right )^{2}}$ .

c) $y'=\frac{\left ( x^{2}+2x+3 \right )'.\left ( 3-4x \right )-\left ( x^{2} +2x+3\right ).\left ( 3-4x \right )'}{\left ( 3-4x \right )^{2}}$ = $\frac{\left ( 2x+2 \right ).\left ( 3-4x \right )-\left ( x^{2}+2x+3 \right ).(-4)}{(3-4x)^{2}}$ = $\frac{-2(2x^{2}-3x-9)}{(3-4x)^{2}}$ .

d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)

SG

Sách Giáo Khoa

4 tháng 4 2017

Bằng định nghĩa, tìm đạo hàm của các hàm số sau :

a) \(y=7+x-x^2\) tại \(x_0=1\)

b) \(y=x^3-2x+1\) tại \(x_0=2\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

MH

Minh Hải

9 tháng 4 2017

a) Giả sử ∆x là số gia của số đối tại x₀= 1. Ta có:

∆y = f(1 + ∆x) - f(1) = 7 + (1 + ∆x) - (1 + ∆x)² - (7 + 1 - 1²) = -(∆x)²- ∆x ;

$\frac{\Delta y}{\Delta x}$ = - ∆x - 1 ; $\lim_{\Delta x\rightarrow 0}$ $\frac{\Delta y}{\Delta x}$ = $\lim_{\Delta x\rightarrow 0}$ (- ∆x - 1) = -1.

Vậy f'(1) = -1.

b) Giả sử ∆x là số gia của số đối tại x₀= 2. Ta có:

∆y = f(2 + ∆x) - f(2) = (2 + ∆x)³- 2(2 + ∆x) + 1 - (2³ - 2.2 + 1) = (∆x)³ + 6(∆x)² + 10∆x;

$\frac{\Delta y}{\Delta x}$ = (∆x)² + 6∆x + 10; $\lim_{\Delta x\rightarrow 0}$ $\frac{\Delta y}{\Delta x}$ = $\lim_{\Delta x\rightarrow 0}$ [(∆x)² + 6∆x + 10] = 10.

Vậy f'(2) = 10.