NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 1 2017
Gọi SO là đường cao của hình chóp
Khi đó △ AOB là tam giác đều cạnh
AB=6cm ⇒ OA=6cm
Trong tam giác vuông SOA áp dụng pi-ta-go ta tính được SO = 8cm
Vậy chọn đáp án B
31 tháng 7 2023
Sxq=1/2*40*13=20*13=260cm2
Độ dài cạnh ở đáy là 40/4=10cm
V=10^2*12=1200cm3
CM
5 tháng 12 2019
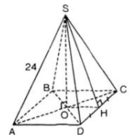
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 -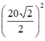 
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
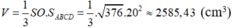
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 –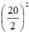 
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
CM
13 tháng 2 2017
a)
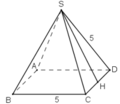
Ta có: các mặt bên của hình chóp đều là những tam giác đều cạnh 5cm. Đường cao của mỗi mặt bên:
b)
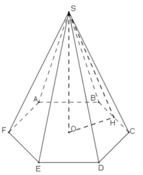
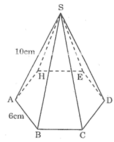
Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên 10cm, cạnh đáy 6cm.
Diện tích toàn phần của hình chóp là:
Stp = Sxq + Sđ = 171,72 + 93,6 = 265,32(cm2)
CM
28 tháng 2 2019
Chọn đáp án A
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
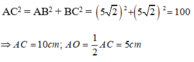
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm
16 tháng 5 2018
a) Ta có các mặt bên của hình chóp đều là những tam giác đều cạnh 5cm. Đường cao của mỗi mặt bên :
SH = √SC2−HC2SC2−HC2
= √52−2,5252−2,52 = √18,75 ≈ 4,33 (cm)
Diện tích xung quanh hình chóp:
Sxq = p.d = 1212.5.4. 4,33 = 43,3 (cm2)
Diện tích đáy hình chóp:
Sđ = a 2 = 52 = 25(cm2)
Diện tích toàn phần hình chóp:
Stp = Sxq + Sđ = 43,3 + 25 = 68,3 (cm2)
Xem thêm tại: http://loigiaihay.com/bai-48-trang-124-sgk-toan-lop-8-tap-2-c43a6297.html#ixzz5FeMLVE4p
16 tháng 5 2018
Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên 5cm, cạnh đáy 6cm.
Đường cao SH của mặt bên là :
SH = √SA2−AH2SA2−AH2 = √52−3252−32 = √16 = 4 (cm)
Diện tích xung quanh hình chóp:
Sxq = p.d = 1212.6.6 .4 =72 (cm2)
Đáy của hình chóp là lục giác đều. Diện tích lục giác bằng 6 lần diện tích tam giác đều ABO.
Chiều cao của tam giác đều là:
OH = √OB2−BH2OB2−BH2 = √62−3262−32 = √27 ≈ 5,2 (cm)
Diện tích đáy hình chóp:
Sđ = 6.1212.6.5,2 = 93,6 (cm2)
Diện tích toàn phần hình chóp:
Stp = Sxq + Sđ =72 + 93,6 =165,6 (cm2)
linh hk bt lm
25 tháng 8 2023
Kẻ SO vuông góc (ABC)
=>SO là trung đoạn của hình chóp S.ABC và O là tâm của ΔABC
Gọi giao của AO với BC là E
=>AO vuông góc BC tại E
ΔABC đều có AE là đường cao và O là tâm
nên AO=2/3AE và \(AE=\dfrac{6\sqrt{3}}{2}=3\sqrt{3}\left(cm\right)\)
=>\(AO=2\sqrt{3}\left(cm\right)\)
ΔSAO vuông tại O
=>SO^2+OA^2=SA^2
=>\(SO^2+12=5^2\)
=>\(SO=\sqrt{13}\left(cm\right)\)
\(S_{XQ}=\dfrac{1}{2}\sqrt{13}\cdot6\cdot3=9\sqrt{13}\)
=>Không có câu nào đúng
HT
2
15 tháng 3 2022
Sorry cho sửa lại
Thể tích hình chóp là: \(V=\dfrac{1}{3}\cdot4\cdot\dfrac{27\sqrt{3}}{4}=9\sqrt{3cm^3}\)