Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a: có 2 bước
bước 1 : tính cạnh BH
ta có: AB = AC = 7 +2 =9
theo định lý Py -ta -go:
ta có : BH2 = AB2- HB2
BH2= 92-72
=>BH=\(\sqrt{32}\)
bước 2: tính cạnh BC
theo định lí Py-ta-go
ta có: BH2 + HC2=BC2
=>BC2= \(\sqrt{32}\)2 + 22 =36
=> BC = \(\sqrt{36}\) = 6
câu b: có 2 bước
bước 1: tìm cạnh BH
ta có AB = AC= 4+1=5
theo định lí Py-ta-go
ta có BH2 = AB2 - AH2
BH2 = 52-42
=> BH= 3
bước 2 : tìm cạnh BC
theo định lí Py-ta-go
ta có : BC2= HC2+BH2
BC2= 12+32
=>BC=\(\sqrt{10}\)
a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC =7 + 2 = 9 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go,ta có:
AB2 = BH2 + AH2
\(\Rightarrow\)92 = BH2 + 72
BH2 = 92 - 72
BH2 = 81 - 49
BH2 = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = BH2 + HC2
\(\Rightarrow\)BC2 = \(\sqrt[]{32}\)2 + 22
BC2 = 32 + 4
BC2 = 36\(\Rightarrow\)BC = 6 (cm)
b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC = 4 + 1 = 5 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go, ta có:
AB2 = HB2 + AH2
\(\Rightarrow\)52 = HB2 + 42
HB2 = 52 - 42
HB2 = 25 - 16
HB2 = 9 \(\Rightarrow\)HB = 3 (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = HC2 + BH2
\(\Rightarrow\)BC2 = 12 + 32
BC2 = 1 + 9
BC2 = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)

a)Tam giác ABC cân tại A =) AB=AC=7+2=9(cm)
Xết tam giác AHB có góc H=900
Theo định lí py-ta-go, ta có::
AB2- AH2= BH2
(=)81-49=BH2
(=)32=BH2
Xét tam giác BHC có góc H=900
Theo định lí pu-ta-go, ta có:
BH2+HC2 =BC2
(=) 32+22 =BC2
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
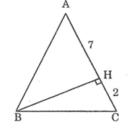
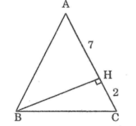

Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm

Giải:
a)
A B C H 1 2 Độ dài cạnh AC là:
AH+HX=7+2=9(cm)
Vì \(\Delta\) ABC là \(\Delta\) cân nên có hai cạnh AB và AC bằng nhau.
Áp dụng định lí Pi-ta-go vào \(\Delta\) ABC(góc H1=90 độ), ta có:
BC^2=BA^2+CA^2
Thay: BC^2=9^2+9^2
BC^2=81+81
=162
=> BC= \(\sqrt{162}\) = 9\(\sqrt{2}\)
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên phải: AH = 4cm; HC = 1cm
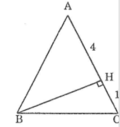

Tam giác ABC cân tại A nên ta có: AB=AC= AH + HC =4+1=5
Trong tam giác vuông BHA ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=52-42=25-16=9
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2
BC2=9+1=10 =>BC=√10

a)Áp dụng định lý Py-ta-go vào tam giác vuông ABH ta có:
AB2=AH2+BH2
72+BH2=92
\(\Rightarrow\)BH2=92-72
BH2=32
\(\Rightarrow\)BH=\(\sqrt{32}\)
Áp dụng định lý Py-ta-go vào tam giác vuông HBC ta có:
BC2=BH2+HC2
32+4=BC2
BC2=36
\(\Rightarrow\)BC=\(\sqrt{36}\)=6
Vậy cạnh đáy=6cm
b) Giải tương tự câu a ta được cạnh đáy =\(\sqrt{10}\)cm
Chúc bạn học tốt!