
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

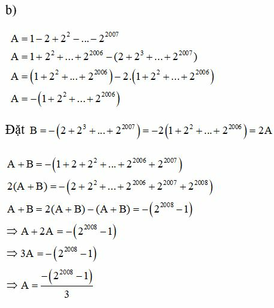
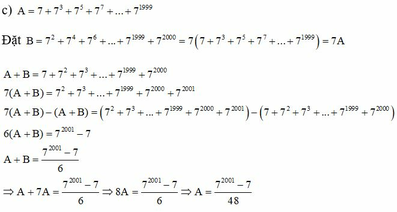

mình chỉ làm câu b) thôi nhé.Còn các câu khác cậu làm tương tự
B=1+2^2+2^4+2^6+2^8+2^10+...+2^200
2^2B=2^2.(1+2^2+2^4+2^6+2^8+2^10+...+2^200)
2^2B=2^2+2^4+2^6+2^8+2^10+2^12+...+2^201
2^2B-2B=(2^2+2^4+2^6+2^8+2^10+2^11+...+2^201)-(1+2^2+2^4+2^6+2^8+2^10+...+2^200)
2B=2^201-1
B=(2^201-1):2

Đăt A = \(\frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+......+\frac{1}{7^{100}}\)
\(\Rightarrow7A=1+\frac{1}{7}+\frac{1}{7^2}+.....+\frac{1}{7^{100}}\)
\(\Rightarrow7A-A=1-\frac{1}{7^{100}}\)
\(\Rightarrow6A=1-\frac{1}{7^{100}}\)
\(\Rightarrow A=\frac{1-\frac{1}{7^{100}}}{6}\)

a) A=\(\frac{178}{179}+\frac{179}{180}+\frac{183}{181}\)
ta có :
\(A=\left(1-\frac{1}{179}\right)+\left(1-\frac{1}{180}\right)+\left(1+\frac{2}{181}\right)\)
\(\Rightarrow A=\left(1+1+1\right)-\left(\frac{1}{179}-\frac{1}{180}+\frac{2}{181}\right)\)
\(\Rightarrow A=3-\left(\frac{1}{179}-\frac{1}{180}+\frac{2}{181}\right)< 3\)
Vậy \(A< 3\)
a. Ta có :
\(\frac{178}{179}< 1\left(\frac{1}{179}\right)\)
\(\frac{179}{180}< 1\left(\frac{1}{180}\right)\)
\(\frac{183}{181}>1\left(\frac{3}{181}\right)\left(1\right)\)
Mà \(\frac{3}{181}>\frac{1}{179}+\frac{1}{180}\left(=\frac{359}{32220}< \frac{3}{181}\right)\left(2\right)\)
Từ \(\left(1\right)\&\left(2\right)\Rightarrow\frac{178}{179}+\frac{179}{180}+\frac{183}{181}< 1+1+1\)
Vậy \(A< 3\)

A=1−3+5−7+...+2001−2003+2005S=1−3+5−7+...+2001−2003+2005
=(1−3)+(5−7)+...+(2001−2003)+2005=(1−3)+(5−7)+...+(2001−2003)+2005(Có 1002 cặp)
=(−2).1002+2005=(−2).1002+2005
=−2004+2005=−2004+2005
=1

\(A=5+5^2+5^3+5^4+...+5^{2004}\)
\(5A=5^2+5^3+5^4+5^5+...+5^{2005}\)
\(5A-A=\left(5^2+5^3+5^4+5^5+...+5^{2005}\right)-\left(5+5^2+5^3+5^4+...+5^{2004}\right)\)
\(4A=5^{2005}-5\)
\(A=\dfrac{5^{2005}-5}{4}\)
\(B=7^1+7^2+7^3+....+7^{2015}\)
\(7B=7^2+7^3+7^4+....+7^{2016}\)
\(7B-B=\left(7^2+7^3+7^4+...+7^{2016}\right)-\left(7+7^2+7^3+....+7^{2015}\right)\)
\(6B=7^{2016}-7\)
\(B=\dfrac{7^{2016}-7}{6}\)
\(C=4^5+4^6+4^7+...+4^{2016}\)
\(4C=4^6+4^7+4^8+...+4^{2017}\)
\(4C-C=\left(4^6+4^7+4^8+...+4^{2017}\right)-\left(4^5+4^6+4^7+...+4^{2016}\right)\)
\(3C=4^{2017}-4^5\)
\(C=\dfrac{4^{2017}-4^5}{3}\)
A = 5 + 52 + 53 + 54 + ... + 52004
5A = 52 + 53 + 54 + 55 + ... + 52005
5A - A = 52005 - 5
4A = 52005 - 5
A = (52005 - 5) : 4
B = 71 + 72 + 73 + ... + 72015
7B = 72 + 73 + 74 + ... + 72016
7B - B = 72016 - 7
6B = 72016 - 7
B = (72016 - 7) : 6
C = 45 + 46 + 47 + ... + 42016
4C = 46 + 47 + 48 + ... + 42017
4C - C = 42017 - 45
3C = 42017 - 45
C = (42017 - 45) : 3

a)Gọi số mới là 664abc (0=<a,b,c=<9)
ta có 664abc chia hết cho 9 nên (6+6+4+a+b+c)\(⋮\)9 \(\Leftrightarrow\left(16+a+b+c\right)⋮9\)
mặt khác số đó còn chia hết cho 11
nên (6+4+b-6-a-c)\(⋮11\Leftrightarrow\left(4+b-a-c\right)⋮11\)mà 4+b-c-a có GTLN là 13 vậy 4+b-a-c=11
ta thấy \(0\le a,b,c\le9\Rightarrow16+a+b+c\le43\Rightarrow16+a+b+c\in\left\{9;18;27;36\right\}\)
| 16+a+b+c | 9 | 18 | 27 | 36 |
| 4+b-a-c | 11 | 11 | 11 | 11 |
| b | 0(t/m) | 4,5(L) | 9(t/m) | 13,5(L) |
số đó cx chia hết cho 5 nên c=(0;5)
TH1 b=0 thì a+c=-7(vô lý)
Th2:b=9 thì a+c=2
nên c chỉ có thể là 0
với c=0 thì a=2
Vậy số thêm vào là 290 và số sau khi thêm vào là 664290