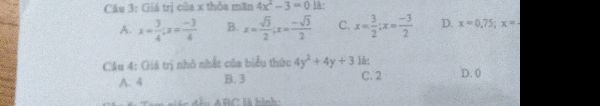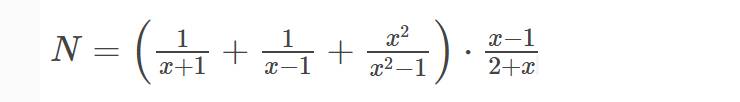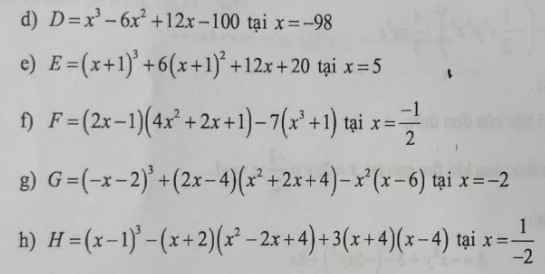Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) A = (x - 5)(x² + 5x + 25) - (x - 2)(x + 2) + x(x² + x + 4)
= x³ - 125 - x² + 4 + x³ + x² + 4x
= (x³ + x³) + (-x² + x²) + 4x + (-125 + 4)
= 2x³ + 4x - 121
b) Tại x = -2 ta có:
A = 2.(-2)³ + 4.(-2) - 121
= 2.(-8) - 8 - 121
= -16 - 129
= -145
c) x² - 1 = 0
x² = 1
x = -1; x = 1
*) Tại x = -1 ta có:
A = 2.(-1)³ + 4.(-1) - 121
= 2.(-1) - 4 - 121
= -2 - 125
= -127
*) Tại x = 1 ta có:
A = 2.1³ + 4.1 - 121
= 2.1 + 4 - 121
= 2 - 117
= -115

a: ĐKXĐ: \(x\notin\left\{1;-1;-2\right\}\)
b: \(N=\left(\dfrac{1}{x+1}+\dfrac{1}{x-1}+\dfrac{x^2}{x^2-1}\right)\cdot\dfrac{x-1}{x+2}\)
\(=\left(\dfrac{1}{x+1}+\dfrac{1}{x-1}+\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x-1}{x+2}\)
\(=\dfrac{x-1+x+1+x^2}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{x-1}{x+2}\)
\(=\dfrac{x^2+2x}{\left(x+2\right)\left(x+1\right)}=\dfrac{x}{x+2}\)
c: |x|=2
=>x=2(nhận) hoặc x=-2(loại)
Thay x=2 vào N, ta được:
\(N=\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)

d: \(D=x^3-6x^2+12x-100\)
\(=x^3-6x^2+12x-8-92\)
\(=\left(x-2\right)^3-92\)
Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)
e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)
\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)
\(=\left(x+1+2\right)^3\)
\(=\left(x+3\right)^3\)
Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)
f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=x^3-8\)
Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)
\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)
\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)
\(=-2x^3-12x-8+2x^3-16=-12x-24\)
Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)
h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)
\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)
\(=3x-57\)
Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)

a: Ta có: \(P=\left(x-1\right)^2-4x\left(x+1\right)\left(x-1\right)+3\)
\(=x^2-2x+1-4x\left(x^2-1\right)+3\)
\(=x^2-2x+4-4x^3+4x\)
\(=-4x^3+x^2+2x+4\)
b: Thay x=-2 vào P, ta được:
\(P=-4\cdot\left(-8\right)+4-4+4=36\)

\(a.a\ne\pm1\)
\(b.K=\dfrac{1}{a+1}+\dfrac{2}{a^2-1}=\dfrac{a-1}{\left(a-1\right)\left(a+1\right)}+\dfrac{2}{\left(a-1\right)\left(a+1\right)}=\dfrac{a+1}{\left(a-1\right)\left(a+1\right)}=\dfrac{1}{a-1}\)
\(c.K=\dfrac{1}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2\)

a: Khi x=2 và y=-3 thì \(x^2+2y=2^2+2\cdot\left(-3\right)=4-6=-2\)
b: \(A=x^2+2xy+y^2=\left(x+y\right)^2\)
Khi x=4 và y=6 thì \(A=\left(4+6\right)^2=10^2=100\)
c: \(P=x^2-4xy+4y^2=\left(x-2y\right)^2\)
Khi x=1 và y=1/2 thì \(P=\left(1-2\cdot\dfrac{1}{2}\right)^2=\left(1-1\right)^2=0\)

a, ĐKXĐ:\(\left\{{}\begin{matrix}x^2-1\ne0\\x+1\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\pm1\\x\ne-1\\x\ne1\end{matrix}\right.\Leftrightarrow x\ne\pm1\)
b, \(P=\dfrac{2x^2}{x^2-1}+\dfrac{x}{x+1}-\dfrac{x}{x-1}\)
\(\Rightarrow P=\dfrac{2x^2}{\left(x+1\right)\left(x-1\right)}+\dfrac{x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}-\dfrac{x\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x^2}{\left(x+1\right)\left(x-1\right)}+\dfrac{x^2-x}{\left(x+1\right)\left(x-1\right)}-\dfrac{x^2+x}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x^2+x^2-x-x^2-x}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x^2-2x}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x}{x+1}\)
c, Thay x=2 vào P ta có:
\(P=\dfrac{2x}{x+1}=\dfrac{2.2}{2+1}=\dfrac{4}{3}\)
Bài `1:`
`a)`
Để `P` có nghĩa thì:
`{(x^2-1\ne0),(x+1\ne0),(x-1\ne0):}`
`<=>x\ne+-1`
`b)`
`P=(2x^2)/(x^2-1)+x/(x+1)-x/(x-1)(x\ne+-1)`
`P=(2x^2)/((x-1)(x+1))+(x.(x-1))/((x+1)(x-1))-(x.(x+1))/((x-1)(x+1))`
`P=(2x^2+x^2-x-x^2-x)/((x-1)(x+1))`
`P=(2x^2-2x)/((x-1)(x+1))`
`P=(2x.(x-1))/((x-1)(x+1))=2x/(x+1)`
`c)`
Với `x=2`
`P=(2.2)/(2+1)=4/3`

a: \(M=\dfrac{18+5x+15+3x-9}{\left(x+3\right)\left(x-3\right)}=\dfrac{8x+24}{\left(x+3\right)\left(x-3\right)}=\dfrac{8}{x-3}\)
b: Thay x=11 vào M, ta được:
\(M=\dfrac{8}{11-3}=1\)
a) \(M=\dfrac{18}{x^2-9}+\dfrac{5}{x-3}+\dfrac{3}{x+3}.\left(x\ne\pm3\right).\)
\(M=\dfrac{18}{\left(x-3\right)\left(x+3\right)}+\dfrac{5}{x-3}+\dfrac{3}{x+3}=\dfrac{18+5\left(x+3\right)+3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{18+5x+15+3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{24+8x}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{8\left(3+x\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{8}{x-3}.\)
b) Thay \(x=11\left(TM\right)\) vào biểu thức M:
\(\dfrac{8}{11-3}=\dfrac{8}{8}=1.\)