
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1 2 2 < 1 1.2 ; 1 3 2 < 1 2.3 ; 1 4 2 < 1 3.4 ; ... ; 1 10 2 < 1 9.10
⇒ 1 2 2 + 1 3 2 + 1 4 2 + 1 10 2 < 1 1.2 + 1 2.3 + 1 3.4 + ... + 1 9.10 < 1.

1 2 2 + 1 3 2 + 1 4 2 + ... + 1 9 2 > 1 2.3 + 1 3.4 + 1 4.5 + ... + 1 9.10 = 2 5
1 2 2 + 1 3 2 + 1 4 2 + ... + 1 9 2 < 1 1.2 + 1 2.3 + 1 3.4 + 1 8.9 = 8 9

(102 + 112 + 122) : (132 + 142)
= (100 + 121 + 144) :( 169 + 196)
= 365: 365
= 1

Ta có: 102+112+122 = 100 + 121 + 144 = 365
132+142 = 169 + 196 = 365
Vậy 102+112+122 = 132+142

a ) 1 2.3 + 1 3.4 + ... + 1 6.7 = 1 2 − 1 7 < 1 2 .
b ) 4 1.5 + 4 5.9 + 4 9.13 + 4 13.17 + 4 17.21 = 1 − 1 21 < 1. c ) T a c ó 1 2 2 < 1 1.2 ; 1 3 2 < 1 2.3 ; 1 4 2 < 1 3.4 ; ... ; 1 10 2 < 1 9.10 . D o đ ó , 1 2 2 + 1 3 2 + 1 4 2 + 1 10 2 < 1 1.2 + 1 2.3 + 1 3.4 + ... + 1 9.10 < 1.
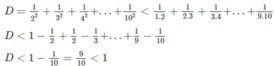
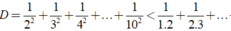
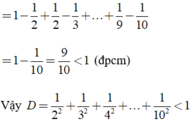
Tính tổng:
\(A=12^2+14^2+...+2010^2=\left(2.6\right)^2+\left(2.7\right)^2+...+\left(2.1005\right)^2\)
\(A=2^2.6^2+2^2.7^2+...+2^2.1005^2=4\left(6^2+7^2+...+1005^2\right)\)
Đặt
\(B=6^2+7^2+...+1005^2=\left(1+5\right)6+\left(1+6\right)7+...+\left(1+1004\right)1005\)
\(B=\left(6+7+...+1005\right)+\left(5.6+6.7+...+1004.1005\right)\)
Đặt \(C=5.6+6.7+...+1004.1005\)
\(3C=5.6\left(7-4\right)+6.7.\left(8-5\right)+...+1004.1005.\left(1006-1003\right)\)
\(=5.6.7-4.5.6+6.7.8-5.6.7+...+1004.1005.1006-1003.1004.1005\)
\(=1004.1005.1006-4.5.6\)
\(\Rightarrow C=\dfrac{1004.1005.1006-4.5.6}{3}=335.1004.1006-2.4.5\)
Mặt khác:
\(6+7+...+1005=\dfrac{1005+6}{2}.1000=1011.500\)
Vậy \(A=4\left(500.1011+335.1004.1006-2.4.5\right)\)
?????????