IL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
IL
2
LN
1
14 tháng 9 2017
\(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4\)
\(\Leftrightarrow x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}-4=0\)
\(\Leftrightarrow\left(x^2-2.x.\frac{1}{x}+\frac{1}{x^2}\right)+\left(y^2-2.y.\frac{1}{y}+\frac{1}{y^2}\right)=0\)
\(\Leftrightarrow\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)(1)
Ta thấy \(\left(x-\frac{1}{x}\right)^2\ge0;\left(y-\frac{1}{y}\right)^2\ge0\forall x;y\) nên \(\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2\ge0\forall x;y\)
Để (1) xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x-\frac{1}{x}\right)^2=0\\\left(y-\frac{1}{y}\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{x}\\y=\frac{1}{y}\end{cases}\Rightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}}\)
Vậy \(x=y=1\)
PN
9 tháng 4 2016
Bài \(1a.\) Tìm \(x,y,z\) biết \(x^2+4y^2=2xy+1\) \(\left(1\right)\) và \(z^2=2xy-1\) \(\left(2\right)\)
Cộng \(\left(1\right)\) và \(\left(2\right)\) vế theo vế, ta được:
\(x^2+4y^2+z^2=4xy\)
\(\Leftrightarrow\) \(x^2-4xy+4y^2+z^2=0\)
\(\Leftrightarrow\) \(\left(x-2y\right)^2+z^2=0\)
Do \(\left(x-2y\right)^2\ge0\) và \(z^2\ge0\) với mọi \(x,y,z\)
nên để thỏa mãn đẳng thức trên thì phải đồng thời xảy ra \(\left(x-2y\right)^2=0\) và \(z^2=0\)
\(\Leftrightarrow\) \(^{x-2y=0}_{z^2=0}\) \(\Leftrightarrow\) \(^{x=2y}_{z=0}\)
Từ \(\left(2\right)\), với chú ý rằng \(x=2y\) và \(z=0\), ta suy ra:
\(2xy-1=0\) \(\Leftrightarrow\) \(2.\left(2y\right).y-1=0\) \(\Leftrightarrow\) \(4y^2-1=0\) \(\Leftrightarrow\) \(y^2=\frac{1}{4}\) \(\Leftrightarrow\) \(y=\frac{1}{2}\) hoặc \(y=-\frac{1}{2}\)
\(\text{*)}\) Với \(y=\frac{1}{2}\) kết hợp với \(z=0\) \(\left(cmt\right)\) thì \(\left(2\right)\) \(\Rightarrow\) \(2.x.\frac{1}{2}-1=0\) \(\Leftrightarrow\) \(x=1\)
\(\text{*)}\) Tương tự với trường hợp \(y=-\frac{1}{2}\), ta cũng dễ dàng suy ra được \(x=-1\)
Vậy, các cặp số \(x,y,z\) cần tìm là \(\left(x;y;z\right)=\left\{\left(1;\frac{1}{2};0\right),\left(-1;-\frac{1}{2};0\right)\right\}\)
\(b.\) Vì \(x+y+z=1\) nên \(\left(x+y+z\right)^2=1\)
\(\Leftrightarrow\) \(x^2+y^2+z^2+2\left(xy+yz+xz\right)=1\) \(\left(3\right)\)
Mặt khác, ta lại có \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\) \(\Rightarrow\) \(xy+yz+xz=0\) \(\left(4\right)\) (do \(xyz\ne0\))
Do đó, từ \(\left(3\right)\) và \(\left(4\right)\) \(\Rightarrow\) \(x^2+y^2+z^2=1\)
Vậy, \(B=1\)
HP
0
26 tháng 11 2017
Bài 1:
x3+y3=152=> (x+y)(x2-xy+y2)=152
Mà x2-xy+y2=19
=> 19(x+y)=152=> x+y=8
Ta cũng có x-y=2
=> x=5;y=3
Bài 2:
x2+4y2+z2=2x+12y-4z-14
=> x2+4y2+z2-2x-12y+4z+14=0
=> (x2-2x+1)+(4y2-12y+9)+(z2+4z+4)=0
=> (x+1)2+(2y-3)2+(z+2)2=0
=> (x+1)2=(2y-3)2=(z+2)2=0
=> x=-1;y=3/2;z=-2
Bài 3\(\left(\frac{1}{x^2+x}-\frac{1}{x+1}\right):\frac{1-2x+x^2}{2014x}=\left(\frac{1}{x\left(x+1\right)}-\frac{1}{x+1}\right):\frac{\left(1-x\right)^2}{2014x}=\frac{1-x}{x\left(x+1\right)}.\frac{2014x}{\left(1-x\right)^2}=\frac{2014}{\left(x+1\right)\left(1-x\right)}=\frac{2014}{1-x^2}\)
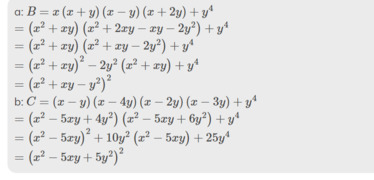
x(x² + x + 1) = 4y(y + 1)
<=> (x + 1)(x² + 1) = (2y + 1)²
Dễ dàng thấy là: x + 1 và x² + 1 nguyên tố cùng nhau nên x + 1 và x² + 1 là 2 số chính phương.
=> x²; x² + 1 là 2 số chính phương liên tiếp
=> x = 0; y = 0 hoặc y = - 1