
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x ≠ 3, x ≠ 4, x ≠ 5, x ≠ 6.
Ta có: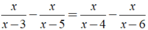
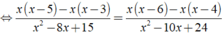
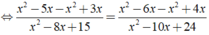
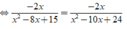
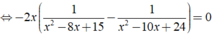
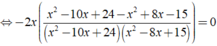
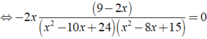
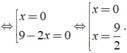
Vậy phương trình đã cho có nghiệm là x = 0;x = 9/2.

a: x(x+5)^2=x+5
=>(x+5)(x^2+5x-1)=0
=>x+5=0 hoặc x^2+5x-1=0
=>\(x\in\left\{-5;\dfrac{-5+\sqrt{29}}{2};\dfrac{-5-\sqrt{29}}{2}\right\}\)
b: x(x-2)=(x-2)
=>(x-2)(x-1)=0
=>x=2 hoặc x=1


\(x^2\left(x-5\right)+x-5=0\)
\(\Rightarrow x^2\left(x-5\right)+\left(x-5\right)=0\)
\(\Rightarrow\left(x-5\right)\left(x^2-1\right)=0\)
\(\Rightarrow\left(x-5\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-5=0\\x-1=0\\x+1=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=5\\x=1\\x=-1\end{matrix}\right.\)
\(x^2\left(x-5\right)+x-5=0\)
\(\Leftrightarrow x-5=0\)
hay x=5
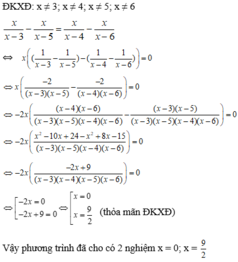
\(\left(6-x\right)^2=x-6\)\(< =>\left(6-x\right)^2+6-x=0\)
\(< =>\left(6-x\right)\left(6-x+1\right)=0\)
\(< =>\orbr{\begin{cases}x=6\\x=7\end{cases}}\)
Trả lời:
\(x-6=\left(6-x\right)^2\)
\(\Leftrightarrow\left(x-6\right)-\left(6-x\right)^2=0\)
\(\Leftrightarrow\left(x-6\right)-\left(x-6\right)^2=0\)
\(\Leftrightarrow\left(x-6\right)\left(1-x+6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(7-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-6=0\\7-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=6\\x=7\end{cases}}}\)
Vậy x = 6; x = 7 là nghiệm của pt.