Tìm x ∈ Q, biết rằng: (x + (1/2))2 = 1/16

GV

Gốc Việt

27 tháng 6 2017 - olm

tìm x thuộc Q, biết rằng :

a) \(\left(x-\frac{1}{2}\right)^2=0\)

b)\(\left(x-2\right)^2=1\)

c) \(\left(2x-1\right)^3=-8\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

TT

Thanh Tùng DZ

27 tháng 6 2017

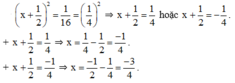
a) \(\left(x-\frac{1}{2}\right)^2=0\)

\(x-\frac{1}{2}=0\)

\(x=0+\frac{1}{2}\)

\(x=\frac{1}{2}\)

b) \(\left(x-2\right)^2=1\)

\(\left(x-2\right)^2=1^2\)

\(x-2=1\)

\(x=1+2\)

\(x=3\)

c) \(\left(2x-1\right)^3=\left(-8\right)\)

\(\left(2x-1\right)^3=\left(-2\right)^3\)

\(2x-1=\left(-2\right)\)

\(2x=\left(-2\right)+1\)

\(2x=-1\)

\(x=-\frac{1}{2}\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\left(x+\frac{1}{2}\right)^2=\left(\frac{1}{4}\right)^2\)

\(x+\frac{1}{2}=\frac{1}{4}\)

\(x=\frac{1}{4}-\frac{1}{2}\)

\(x=-\frac{1}{4}\)

Đúng(0)

LT

lê thị thu huyền

27 tháng 6 2017

a) \(\left(x-\frac{1}{2}\right)^2=0\)

\(\Leftrightarrow x-\frac{1}{2}=0\)

\(\Leftrightarrow x=\frac{1}{2}\)

b) \(\left(x-2\right)^2=1\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=1\\x-2=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)

c) \(\left(2x-1\right)^2=-8\)

\(\Leftrightarrow2x-1=-2\)

\(\Leftrightarrow2x=-1\)

\(\Leftrightarrow x=-\frac{1}{2}\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\Rightarrow\orbr{\begin{cases}x+\frac{1}{2}=\frac{1}{4}\\x+\frac{1}{2}=-\frac{1}{4}\end{cases}\Rightarrow\orbr{\begin{cases}x=-\frac{1}{4}\\x=-\frac{3}{4}\end{cases}}}\)

Đúng(0)

NT

Nguyễn Thị Đỗ Quyên

10 tháng 7 2019 - olm

1. tìm x biết rằng: a.\(x^3=-27\)b\(\left(2x-1\right)^3=8\).c.\(x^2=x^5\)d.\(\left(x-2\right)^2=16\)n.\(\left(2x-3\right)^2=9\)y

#Hỏi cộng đồng OLM #Toán lớp 7

1

NT

Nguyễn Thị Đỗ Quyên

10 tháng 7 2019

chữ y đằng sau số 9 bỏ chỉ có ssó 9 thôi

Đúng(0)

SG

Sách Giáo Khoa

10 tháng 5 2017

Tìm \(x\in\mathbb{Q}\), biết rằng :

a) \(\left(x-\dfrac{1}{2}\right)^2=0\)

b) \(\left(x-2\right)^2=1\)

c) \(\left(2x-1\right)^3=-8\)

d) \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

TN

Trần Ngọc Bích Vân

10 tháng 6 2017

a) \(\left(x-\dfrac{1}{2}\right)^2=0\Rightarrow x-\dfrac{1}{2}=0\Rightarrow x=\dfrac{1}{2}\)

b) Vì \(\left(x-2\right)^2=1\Rightarrow\left\{{}\begin{matrix}x-2=2\\x-2=-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)

Vậy x = 4 hoặc x = 0

c) Vì \(\left(2.x-1\right)^3=-8\Rightarrow2.x-1=-2\Rightarrow2.x=-1\Rightarrow x=-\dfrac{1}{2}\)

d) Vì \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{1}{4}\\x+\dfrac{1}{2}=-\dfrac{1}{4}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{3}{4}\end{matrix}\right.\)

Đúng(0)

MP

Mysterious Person

23 tháng 6 2017

a) \(\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)

b) \(\left(x-2\right)^2=1\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

c) \(\left(2x-1\right)^3=-8\Leftrightarrow2x-1=-2\Leftrightarrow2x=-1\Leftrightarrow x=\dfrac{-1}{2}\) d) \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\Leftrightarrow x+\dfrac{1}{2}=\dfrac{1}{4}\Leftrightarrow x=\dfrac{-1}{4}\)

Đúng(0)

TN

Toàn Nguyễn

14 tháng 7 2016 - olm

Tìm x thuộc Q, biết rằng:

a) \(\left(x-\frac{1}{2}\right)^2=0\)

b) \(\left(x-2\right)^2=1\)

c) \(\left(2x-1\right)^3=-8\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

OI

o0o I am a studious person o0o

14 tháng 7 2016

a) \(\left(x-\frac{1}{2}\right)^2=0\)

\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=\frac{1}{2}\end{cases}}\)

b) \(\left(x-2\right)^2=1\)

\(\Leftrightarrow\left(x-2\right)^2-1=0\)

\(\Leftrightarrow\left(x-2-1\right)\left(x-2+1\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)

c) \(\left(2x-1\right)^3=-8\)

\(\Leftrightarrow2x-1=-2\)

\(\Leftrightarrow2x=-1\)

\(\Leftrightarrow x=\frac{-1}{2}\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\Rightarrow x+\frac{1}{2}=\frac{1}{4}\)

\(\Rightarrow x=-\frac{1}{4}\)

Đúng(0)

K

kakashi

14 tháng 7 2016

a>(x-1/2)^2=0

(x-1/2)^2=0^2

=>x-1/2=0

x=1/2

b>(x-2)^2=1

(x-2)^2=1^2

=>x-2=1

x=3

(2x-1)^3=-8

=>(2x-1)^3=-2^3

=>2x-1=-2

2x=-1

x=-0,5

d>(x+1/2)^2=1/16

(x+1/2)^2=(1/4)^2

=>x+1/2=1/4

x=1/4-1/2

x=-1/4

chuc ban may man trong cuoc song!!!!!

Đúng(0)

NT

Nguyễn Thị Đỗ Quyên

14 tháng 7 2019 - olm

bài 1: tìm x biết rằng:

a. \(x^3=-27\) b.\(\left(2x-1\right)^3=8\) c.\(x^3=x^5\) d.\(\left(x-2\right)^2=16\) g.\(\left(2x-3\right)^2=9\) y.\(3x^3-4x=0\)

#Hỏi cộng đồng OLM #Toán lớp 7

1

K

KAl(SO4)2·12H2O

14 tháng 7 2019

a) x³ = -27

<=> -3³ = -27

=> x = -3

b) (2x - 1)³ = 8

<=> 8x³ - 12x² + 6x - 1 = 8

<=> 8x³ - 12x² + 6x - 1 - 8 = 0

<=> (2x - 3)(4x² + 3) = 0

<=> 2x - 3 = 0 hoặc 4x² + 3 = 0

2x = 0 + 3

2x = 3

x = 3/2

=> x = 3/2

c) x³ = x⁵

<=> x³ - x⁵ = 0

<=> x³(1 - x²) = 0

<=> x = 0; 1; -1

=> x = 0; 1; -1

d) (x - 2)² = 16

<=> (x - 2)² = 4²

<=> x - 2 = 4 hoặc x - 2 = -4

x = 4 + 2 x = -4 + 2

x = 6 x = -2

=> x = 6; -2

g) (2x - 3)² = 9

<=> (2x - 3)² = 3²

<=> 2x - 3 = 3 hoặc 2x - 3 = -3

2x = 3 + 3 2x = -3 + 3

2x = 6 2x = 0

x = 3 x = 0

=> x = 3; 0

y) 3x³ - 4x = 0

<=> x(3x - 4) = 0

<=> x = 0 hoặc 3x - 4 = 0

3x = 0 + 4

3x = 4

x = 4/3

Đúng(0)

NM

Nguyễn Mai

11 tháng 11 2016 - olm

Tìm số tự nhiên x biết rằng

a) \(5^x+5^{x+2}=650\)

b) \(3^{x-1}+5.3^{x-1}=16\)

#Hỏi cộng đồng OLM #Toán lớp 7

1

NQ

Nguyễn Quang Đức

11 tháng 11 2016

\(a,5^x+5^{x+2}=650\Leftrightarrow5^x+5^x+5^2=650\Leftrightarrow5^x.26=650\Leftrightarrow5^x=5^2\Leftrightarrow x=2\) x=2

b,Với x=0 khi đó 3^0-1+5.3^0-1=2 (loại)

Với x=1 khi đó 3^1+5.3^1=18 (loại)

Với x=2 khi đó 5.3^x-1>16 (loại)

Vậy không có x thỏa mãn

Đúng(0)

PH

pham ha my

13 tháng 8 2018 - olm

tìm số nguyên x biết

1/ 2\(^x\)= 4\(^5\). 4\(^3\)

2/ 2\(^x\)= 4\(^6\).16\(^3\)

3/ 2\(^x\)= 4\(^5\).16\(^2\)

#Hỏi cộng đồng OLM #Toán lớp 7

5

U

Umi

13 tháng 8 2018

1/ 2^x = 4⁵.4⁶

=> 2^x = 4^{5 + 6}

=> 2^x = 4¹¹

=> 2^x = (2²)¹¹

=> 2^x = 2²²

=> x = 22

vậy_

2/ 2^x = 4⁶.16³

=> 2^x = (2²)⁶.(2⁴)³

=> 2^x = 2¹².2¹²

=> 2^x = 2^{12 + 12}

=> 2^x = 2²⁴

=> x = 24

3/ 2^x = 4⁵.16²

=> 2^x = (2²)⁵.(2⁴)²

=> 2^x = 2¹⁰.2⁸

=> 2^x = 2^{10 + 8}

=> 2^x = 2¹⁸

=> x = 18

vậy_

Đúng(0)

NB

nguyễn bá lương

13 tháng 8 2018

\(\frac{1}{2^x}=4^5.4^3=4^{5+3}=4^8\)

\(\Rightarrow1=4^8.2^x=2^{2.8+x}=2^{16+x}\)

ta có 1 < 2¹ => 2^16+x < 2¹

=> 2^16+x = 2⁰

=> 16+x=0

=> x= -16

Đúng(0)

MM

Mai Mèo

20 tháng 8 2017

tìm x\(\in\)Q biết rằng

a)\(\left(x-\dfrac{1}{2}\right)^2=0\)

b)\(\left(x-2\right)^2=1\)

c)\(\left(2x-1\right)^3=-8\)

d)\(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

1

MP

Mysterious Person

20 tháng 8 2017

a) \(\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\) vậy \(x=\dfrac{1}{2}\)

b) \(\left(x-2\right)^2=1\Leftrightarrow\left[{}\begin{matrix}x-2=\sqrt{1}\\x-2=-\sqrt{1}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

vậy \(x=3;x=1\)

c) \(\left(2x-1\right)^3=-8\Leftrightarrow2x-1=\sqrt[3]{-8}=-2\Leftrightarrow2x=-1\)

\(\Leftrightarrow x=\dfrac{-1}{2}\) \(\) vậy \(x=\dfrac{-1}{2}\)

d) \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\sqrt{\dfrac{1}{16}}\\x+\dfrac{1}{2}=-\sqrt{\dfrac{1}{16}}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{1}{4}\\x+\dfrac{1}{2}=-\dfrac{1}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-3}{4}\end{matrix}\right.\) vậy \(x=\dfrac{-1}{4};x=\dfrac{-3}{4}\)

Đúng(0)

TN

Trần Nghiên Hy

14 tháng 7 2016

Tìm x thuộc Q biết rằng

a) ( x- \(\frac{1}{2}\)) ²= 0

b) ( x-2) ²=1

c) ( 2x-1) ³= -8

d) ( x+ \(\frac{1}{2}\)) ²= \(\frac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

1

PA

Phương An

14 tháng 7 2016

a.

\(\left(x-\frac{1}{2}\right)^2=0\)

\(x-\frac{1}{2}=0\)

\(x=\frac{1}{2}\)

b.

\(\left(x-2\right)^2=1\)

\(x-2=\pm1\)

TH1:

\(x-2=1\)

\(x=1+2\)

\(x=3\)

TH2:

\(x-2=-1\)

\(x=-1+2\)

\(x=1\)

Vậy x = 3 hoặc x = 1

c.

\(\left(2x-1\right)^3=-8\)

\(\left(2x-1\right)^3=\left(-2\right)^3\)

\(2x-1=-2\)

\(2x=-2+1\)

\(2x=-1\)

\(x=-\frac{1}{2}\)

d.

\(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\left(x+\frac{1}{2}\right)^2=\left(\pm\frac{1}{4}\right)^2\)

\(x+\frac{1}{2}=\pm\frac{1}{4}\)

TH1:

\(x+\frac{1}{2}=\frac{1}{4}\)

\(x=\frac{1}{4}-\frac{1}{2}\)

\(x=\frac{1}{4}-\frac{2}{4}\)

\(x=-\frac{1}{4}\)

TH2:

\(x+\frac{1}{2}=-\frac{1}{4}\)

\(x=-\frac{1}{4}-\frac{1}{2}\)

\(x=-\frac{1}{4}-\frac{2}{4}\)

\(x=-\frac{3}{4}\)

Vậy \(x=-\frac{1}{4}\) hoặc \(x=-\frac{3}{4}\)

Đúng(0)

NT

Nguyễn Trần Duy Thiệu

14 tháng 7 2016

HƠI DÀI NHỈ

Đúng(0)

HT

๖ۣۜ๖ۣۜHσàηɠ ๖ۣۜTử ๖ۣۜGĭóッ

21 tháng 10 2020 - olm

Câu hỏi hay

Bài Tập: Tìm số hữu tỉ x biết rằng ( \(\frac{x}{y}\))\(^2\)= 2 ; \(\frac{x}{y}\)= 16.

#Hỏi cộng đồng OLM #Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP