K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
0
AD
2
29 tháng 9 2016
a) \(2,5:4x=0,5:0,2\)
\(2,5:4x=\frac{5}{2}\)
\(4x=2,5:\frac{5}{2}\)
\(4x=1\)
\(x=\frac{1}{4}\)
Vậy \(x=\frac{1}{4}\)
b) \(\frac{1}{5}.x:3=\frac{2}{3}:0,25\)
\(\frac{1}{5}.x:3=\frac{8}{3}\)
\(\frac{1}{5}.x=\frac{8}{3}.3\)
\(\frac{1}{5}.x=8\)
\(x=8:\frac{1}{5}\)
\(x=40\)
Vậy \(x=40\)
29 tháng 9 2016
a) \(\frac{2,5}{4x}=\frac{0,5}{0,2}\)
\(=>4x=\frac{0,2.2,5}{0,5}=1\)
\(=>x=\frac{1}{4}\)
b) \(\frac{1}{5}.\frac{x}{3}=\frac{2}{3}:0,25\)
\(=>\frac{x}{15}=\frac{4}{3}\)
\(=>x=\frac{4.15}{3}=20\)
13 tháng 12 2021
a/|x|-2,5=27,5
=>|x|=27,5+2,5=30
=>x=30 hoặc x=-30
b/\(\dfrac{3}{4}+\dfrac{2}{5}.x=\dfrac{29}{60}\)
=>\(\dfrac{2}{5}.x\)=\(\dfrac{29}{60}-\dfrac{3}{4}\)=\(\dfrac{-4}{15}\)
=>x=\(\dfrac{-4}{15}:\dfrac{2}{5}\)=\(\dfrac{-2}{3}\)
c/(x-1)\(^5\)=-32
=>x-1=-2 vì (-2)\(^5\)=-32
=>x=-2+1=-1
d/\(\dfrac{4}{5}.x+0,5=4.5\)
=>\(\dfrac{4}{5}.x+0,5=20\)
=>\(\dfrac{4}{5}.x=20-0,5=19,5\)
=>\(x=19,5:\dfrac{4}{5}\)=\(\dfrac{195}{8}\)
LM
15 tháng 6 2017
Ta có: (x - 2,5)2014 + |x + y + 0,5| = 0
Mà: (x - 2,5)2014 lớn hơn hoặc bằng 0 và |x + y + 0,5| cũng lớn hơn hoặc bằng 0
Nên để thỏa mãn đẳng thức đã cho thì: (x - 2,5)2014 = 0 và |x + y + 0,5| = 0 => x - 2,5 = 0 và x + y + 0,5 = 0
Với x - 2,5 = 0 => x = 2,5
Thay x = 2,5 vào x + y + 0,5 = 0 => y = -3
3 tháng 8 2016
1)\(x+0,5+x+1,5+x+2,5=33\)
\(\Leftrightarrow3x=33-0,5-1,5-2,5=28,5\)
\(\Leftrightarrow x=9,5\)
2)\(\left(x+0,9\right)\left(1-0,4\right)=2412\)
\(\Leftrightarrow\left(x+0,9\right)\cdot0,6=2412\)
\(\Leftrightarrow x+0,9=4020\)
\(\Leftrightarrow x=1019,1\)
HT
4 tháng 9 2017
Vì |3,4-x| lớn hơn hoặc bằng 0 với mọi x
=> 1,7+|3,4-x| lớn hơn hoặc bằng 1,7+0
=> A lớn hơn hoặc bằng 1,7
Dấu "=" xảy ra <=> |3,4-x|=0
=>3,4-x=0
=> x= 3,4
Vậy min A= 1,7 khi x= 3,4
X
22 tháng 9 2018
\(A=1,7+\left|3,4-x\right|\)
mà \(\left|3,4-x\right|\ge0\forall x\Rightarrow A\ge1,7\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow3,4-x=0\Leftrightarrow x=3,4\)
\(N=\left|x+3,2\right|-2,5\)
mà \(\left|x+3,2\right|\ge0\forall x\Rightarrow N\ge-2,5\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x+3,2=0\Leftrightarrow x=-3,2\)
\(P=5,5+\left|2x-0,5\right|\)
mà \(\left|2x-0,5\right|\ge0\forall x\Rightarrow P\ge5,5\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow2x-0,5=0\Leftrightarrow x=0,25\)
PT
1
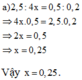
\(\left|x-\dfrac{1}{2}\right|=-\dfrac{5}{2}\)
mà \(\left|x-\dfrac{1}{2}\right|\ge0\forall x\)
nên \(x\in\varnothing\)
ko có x thỏa mãn vì có dấu GTTĐ nên ko thể có kết quả âm