K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
\(\begin{array}{l}a)\sqrt x - 16 = 0\\\sqrt x = 16\\x = {16^2}\\x = 256\end{array}\)
Vậy x = 256
\(\begin{array}{l}b)2\sqrt x = 1,5\\\sqrt x = 1,5:2\\\sqrt x = 0.75\\x = {(0,75)^2}\\x = 0,5625\end{array}\)
Vậy x = 0,5625
\(\begin{array}{l}c)\sqrt {x + 4} - 0,6 = 2,4\\\sqrt {x + 4} = 2,4 + 0,6\\\sqrt {x + 4} = 3\\x + 4 = 9\\x = 5\end{array}\)
Vậy x = 5
10 tháng 8 2017
a) 1
b) 1 hoặc 0
c) 0
d) 2
Căn bản cx đã muộn nên mk làm ngắn gọn, nếu bn cần lời giải chi tiết hãy add mk để có lời giải chi tiết nhé!
YT
1
16 tháng 10 2023
`#3107.101107`
`1/2x + 4/5 = 2x - 8/5`
`=> 1/2x - 2x = -4/5 - 8/5`
`=> -3/2x = -12/5`
`=> x = -12/5 \div (-3/2)`
`=> x = 8/5`
Vậy, `x = 8/5`
_____
`\sqrt{x} = 5`
`=> x = 5^2`
`=> x = 25`
Vậy, `x = 25`
___
`x^2 = 3`
`=> x^2 = (+-\sqrt{3})^2`
`=> x = +- \sqrt{3}`
Vậy, `x \in {-\sqrt{3}; \sqrt{3}}.`
HP
15 tháng 1 2016
|5x-3|-2x=14
=>|5x-3|=14+2x
=>5x-3=14+2x hoặc 5x-3=-14-2x
=>x=17/3 hoặc x=-11/7
=>x ko tồn tại
HP
15 tháng 1 2016
5/x+y/4=1/8
=>5/x=1/8-y/4
=>5/x=1/8-2y/8=(1-2y)/8
=>x.(1-2y)=5.8=40
rồi lập bảng (chú ý là 1-2y là ước lẻ của 40)
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) |x| = 4
\(\left[ {_{x = - 4}^{x = 4}} \right.\)
Vậy \(x \in \{ 4; - 4\} \)
b) |x| = \(\sqrt 7 \)
\(\left[ {_{x = - \sqrt 7 }^{x = \sqrt 7 }} \right.\)
Vậy \(x \in \{ \sqrt 7 ; - \sqrt 7 \} \)
c) ) |x+5| = 0
x+5 = 0
x = -5
Vậy x = -5
d) \(\left| {x - \sqrt 2 } \right|\) = 0
x - \(\sqrt 2 \) = 0
x = \(\sqrt 2 \)
Vậy x =\(\sqrt 2 \)
24 tháng 1 2017
f)
\(A=\sqrt{\frac{\left(x+1\right)}{x-3}}=\sqrt{1+\frac{4}{x-3}}\)
x-3={-4)=> x=-1
AH
Akai Haruma
Giáo viên
6 tháng 11 2023
Lời giải:
Ta thấy: $\sqrt{(x-2024)^2}\geq 0$ với mọi $x\in\mathbb{R}$
$|x+y-4z|\geq 0$ với mọi $x,y,z\in\mathbb{R}$
$\sqrt{5y^2}\geq 0$ với mọi $y\in\mathbb{R}$
Do đó để tổng của chúng bằng $0$ thì bản thân mỗi số đó phải nhận giá trị $0$
Hay:
$\sqrt{(x-2024)^2}=|x+y-4z|=\sqrt{5y^2}=0$
$\Leftrightarrow x=2024; y=0; z=\frac{x+y}{4}=506$
27 tháng 5 2022
ĐKXĐ: x>=0
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\x^2-4=0\end{matrix}\right.\Leftrightarrow x\in\left\{0;2\right\}\)
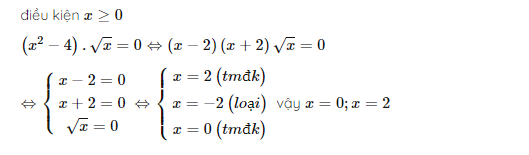
\(\sqrt{x+2}+4=0\)
=> \(\sqrt{x+2}=-4\)
=> x+2 = (-4)2
=> x+2 = 16
=> x = 16 - 2
=> x = 14
SAi mà Hồ Thu Giang