
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


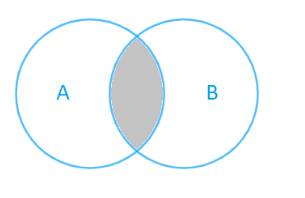
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

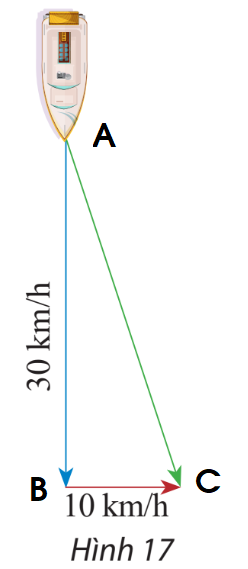
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

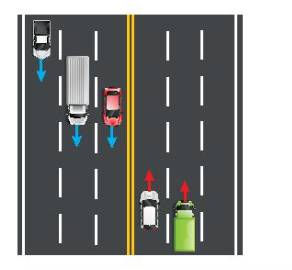
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.

a ) \mathbb{R} \backslash (-3; \, 1]R\(−3;1]=(-∞;-3]∪(1;+∞)
b) (-\infty; \, 1) \backslash [-2; \, 0](−∞;1)\[−2;0]=(- (-\infty; \, 1) \backslash [-2; \, 0]∞;-2)∪(0;1)

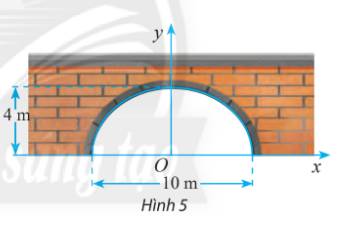
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

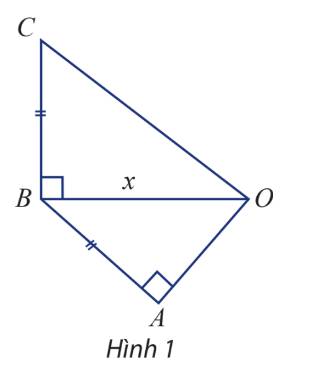
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)
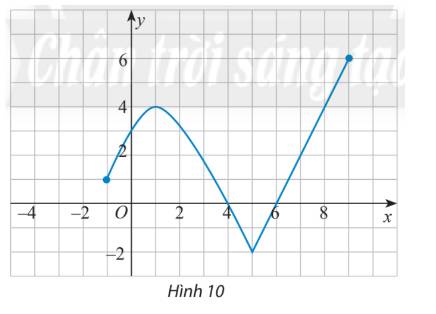



Từ đồ thị, ta có:
Đồ thị hàm số xác định (liền mạch) từ \(x = - 1\) đến \(x = 9\), do đó tập xác định của hàm số là \(D = [ - 1;9].\)
Tập giá trị \(T = \{ y|x \in [ - 1;9]\} \), vậy \(T = [ - 2;6]\)