Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Hàm số y = sin 2x thỏa mãn tính chất trên, các hàm số y = tan x, y = cot x cần điều kiện của x.
Ta có
S 1 = ∫ 0 k e x sin x d x ; S 2 = ∫ k π e x sin x d x S = S 1 + S 2 = ∫ 0 π e x sin x d x
2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2
⇔ S 2 = 2 S 1 2 - 2 S 1 + 1 - S = 0 ⇔ 2 ∫ 0 k e x sin x d x 2 - 2 ∫ 0 k e x sin x d x + 1 - ∫ 0 k e x sin x d x = 0
Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2
Đáp án cần chọn là B
Đáp án B
Phương pháp giải:
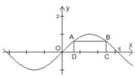
Dựa vào đồ thị hàm số xác định hoành độ điểm D suy ra tung độ điểm A chính là độ dài BC
Lời giải: Gọi 
với 
Gọi 
thuộc đồ thị 
Vì ABCDlà hình chữ nhật 
Khi đó BC = m. Mà 
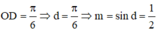
Đáp án B
TXĐ của hàm y = tanx là D = ℝ \ π 2 + k π | k ∈ ℤ nên TXĐ của hàm y = tan 2 x là D = ℝ \ π 4 + k π 2 | k ∈ ℤ
TXĐ của hàm y = cot x là D = ℝ \ k π | k ∈ ℤ nên TXĐ của hàm y = cot 2 x là D = ℝ \ k π 2 | k ∈ ℤ
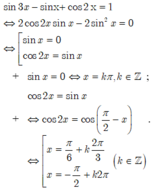
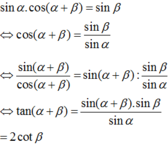
Ta có - 1 ≤ cos 2 x ≤ 1 nên 5 - 3 cos 2 x > 0
Mặt khác 1 + sin 2 x - π 2 ≥ 0
Hàm số xác định khi và chỉ khi
5 - 3 cos 2 x 1 + sin 2 x - π 2 ≥ 0 1 + sin 2 x - π 2 ≠ 0 ⇔ sin 2 x - π 2 ≠ - 1 ⇔ 2 x - π 2 ≠ - π 2 + k 2 π ⇔ x ≠ kπ , k ∈ ℤ
(Để ý rằng bất phương trình (*) luôn đúng)
Tập xác định là D = R ∖ k π , k ∈ ℤ
Dáp án C