Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy hàm số có nghĩa với mọi số thực nên \(D = \mathbb{R}\)
b)
Điều kiện: \(2 - 3x \ge 0 \Leftrightarrow x \le \frac{2}{3}\)
Vậy tập xác định: \(S = \left( { - \infty ;\frac{2}{3}} \right]\)
c) Điều kiện: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
d) Ta thấy hàm số có nghĩa với mọi \(x \in \mathbb{Q}\) và \(x \in \mathbb{R}\backslash \mathbb{Q}\) nên tập xác định: \(D = \mathbb{R}\).

y xác định khi :
X3 - 1 \(\ne\)0
=> X \(\ne\)1.
Vậy TXD : D =R\ {1} hay D = (-\(\infty\);1) \(\cup\)( 1 ; + \(\infty\))

Tham khảo:
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
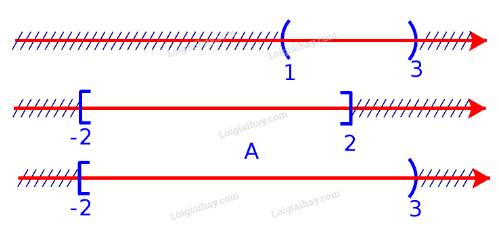
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)
b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
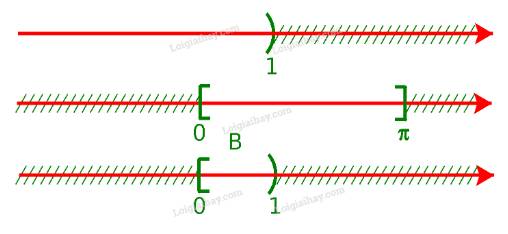
Từ sơ đồ, ta thấy \(B = [0;1)\)
c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
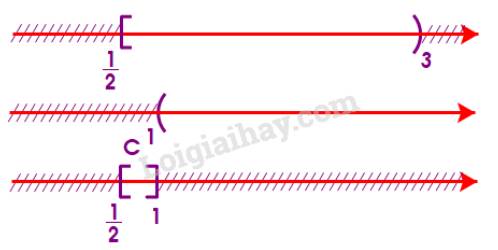
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)
d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
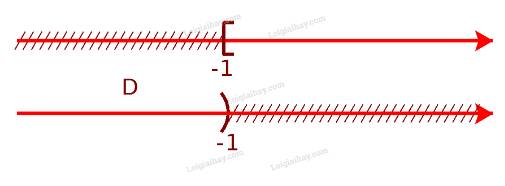
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)

a) Liệt kê các phần tử của tập hợp �={�∈�∣ 2�2+3�+1=0 }A={x∈Z 2x2+3x+1=0 }
Ta có: 2�2+3�+1=0⇔[ �=−12 �=−1 2x2+3x+1=0⇔ x=−21 x=−1 .
Do đó: �={−1}A={−1}.
b) Cho hai tập hợp �={�∈�∣∣�∣>4}A={x∈R∣x∣>4} và �={�∈�∣−5≤�−1<5}B={x∈R−5≤x−1<5}. Xác định tập �=�\�X=B\A.
Ta có:
⚡∣�∣>4⇔[ �>4 �<−4⇒�=(−∞;−4)∪(4;+∞ )∣x∣>4⇔[ x>4x<−4⇒A=(−∞;−4)∪(4;+∞ )

\(C\cap B=[-5;a]\)
mà \(B=\left\{x\in R|-5\le x\le5\right\}\) có độ dài là \(\left|-5\right|+\left|5\right|=10\)
\(\Rightarrow C\cap B=[-5;a]\) có độ dài là \(5\) thì \(a=10:2-5=0\)
\(D\cap B=[b;5]\) có độ dài là 9 thì \(b=10:2-9=-4\)

Để hàm số \(y = \frac{1}{{\sqrt {x - 2} }}\) xác định \( \Leftrightarrow \,\,x - 2 > 0\,\, \Leftrightarrow \,\,x > 2.\)
Vậy tập xác định của hàm số là: \(D = \left( {2; + \infty } \right).\)
Chọn B.