Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

14.
\(log_aa^2b^4=log_aa^2+log_ab^4=2+4log_ab=2+4p\)
15.
\(\frac{1}{2}log_ab+\frac{1}{2}log_ba=1\)
\(\Leftrightarrow log_ab+\frac{1}{log_ab}=2\)
\(\Leftrightarrow log_a^2b-2log_ab+1=0\)
\(\Leftrightarrow\left(log_ab-1\right)^2=0\)
\(\Rightarrow log_ab=1\Rightarrow a=b\)
16.
\(2^a=3\Rightarrow log_32^a=1\Rightarrow log_32=\frac{1}{a}\)
\(log_3\sqrt[3]{16}=log_32^{\frac{4}{3}}=\frac{4}{3}log_32=\frac{4}{3a}\)
11.
\(\Leftrightarrow1>\left(2+\sqrt{3}\right)^x\left(2+\sqrt{3}\right)^{x+2}\)
\(\Leftrightarrow\left(2+\sqrt{3}\right)^{2x+2}< 1\)
\(\Leftrightarrow2x+2< 0\Rightarrow x< -1\)
\(\Rightarrow\) có \(-2+2020+1=2019\) nghiệm
12.
\(\Leftrightarrow\left\{{}\begin{matrix}x-2>0\\0< log_3\left(x-2\right)< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\1< x-2< 3\end{matrix}\right.\)
\(\Rightarrow3< x< 5\Rightarrow b-a=2\)
13.
\(4^x=t>0\Rightarrow t^2-5t+4\ge0\)
\(\Rightarrow\left[{}\begin{matrix}t\le1\\t\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}4^x\le1\\4^x\ge4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\le0\\x\ge1\end{matrix}\right.\)

a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)

1.a/ \(\left\{{}\begin{matrix}3^{x+1}>0\\5^{x^2}>0\end{matrix}\right.\) \(\forall x\) \(\Rightarrow\) pt vô nghiệm
b/ Mình làm câu b, câu c bạn tự làm tương tự, 3 câu này cùng dạng
Lấy ln hai vế:
\(ln\left(3^{x^2-2}.4^{\dfrac{2x-3}{x}}\right)=ln18\Leftrightarrow ln3^{x^2-2}+ln4^{\dfrac{2x-3}{x}}-ln18=0\)
\(\Leftrightarrow\left(x^2-2\right)ln3+\dfrac{2x-3}{x}2ln2-ln\left(2.3^2\right)=0\)
\(\Leftrightarrow x^3ln3-2x.ln3+4x.ln2-6ln2-x.ln2-2x.ln3=0\)
\(\Leftrightarrow x^3ln3-4x.ln3+3x.ln2-6ln2=0\)
\(\Leftrightarrow x.ln3\left(x^2-4\right)+3ln2\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2ln3+2x.ln3+3ln2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\Rightarrow x=2\\x^2ln3+2x.ln3+3ln2=0\left(1\right)\end{matrix}\right.\)
Xét (1): \(\left(x^2+2x\right)ln3=-3ln2\Leftrightarrow x^2+2x=\dfrac{-3ln2}{ln3}=-3log_32\)
\(\Leftrightarrow\left(x+1\right)^2=1-3log_32=log_33-log_38=log_3\dfrac{3}{8}< 0\)
\(\Rightarrow\left(1\right)\) vô nghiệm
\(\Rightarrow\) pt có nghiệm duy nhất \(x=2\)
2/ Pt đã cho tương đương:
\(2017^{sin^2x}-2017^{cos^2x}=cos^2x-sin^2x\)
\(\Leftrightarrow2017^{sin^2x}+sin^2x=2017^{cos^2x}+cos^2x\)
Xét hàm \(f\left(t\right)=2017^t+t\) (\(0\le t\le1\))
\(\Rightarrow f'\left(t\right)=2017^t.ln2017+1>0\) \(\forall t\) \(\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)
\(\Rightarrow sin^2x=cos^2x\Rightarrow cos^2x-sin^2x=0\Rightarrow cos2x=0\)
\(\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Thế k=0; k=1 ta được 2 nghiệm thuộc đoạn đã cho là \(x=\dfrac{\pi}{4};x=\dfrac{3\pi}{4}\)
\(\Rightarrow\) tổng nghiệm là \(T=\dfrac{\pi}{4}+\dfrac{3\pi}{4}=\pi\)

Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a), b) và với đường thẳng y = -1 ở câu c).
a) Xét hàm số y = x3 – 3x2 + 5 . Tập xác định : R.
y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0,x = 2.
Bảng biến thiên:
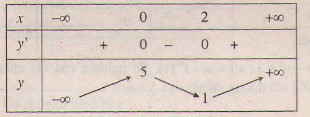
Đồ thị như hình bên.
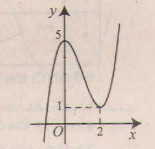
Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
b) Xét hàm số y = -2x3 + 3x2 - 2 . Tập xác định : R.
y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.

Đồ thị như hình bên. Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
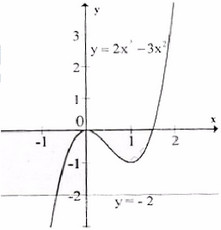
c) Xét hàm số y = f(x) = 2x2 - 2x4. Tập xác định : R.
y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên:
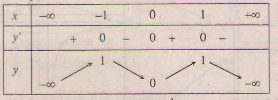
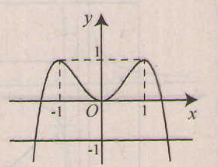
Đồ thị hàm số f(x) và đường thẳng y = -1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.

d) Điều kiện \(\begin{cases}x\ne0\\\log_2\left|x\right|\ge0\end{cases}\)\(\Leftrightarrow\left|x\right|\ge\)1
Phương trình đã cho tương đương với :
\(\log_2\left|x\right|^{\frac{1}{2}}-4\sqrt{\log_{2^2}\left|x\right|}-5=0\)
\(\Leftrightarrow\frac{1}{2}\log_2\left|x\right|-4\sqrt{\frac{1}{4}\log_2\left|x\right|}-5=0\)
Đặt \(t=\sqrt{\frac{1}{2}\log_2\left|x\right|}\) \(\left(t\ge0\right)\) thì phương trình trở thành :
\(t^2-4t-5=0\) hay t=-1 V t=5
Do \(t\ge0\) nên t=5
\(\Rightarrow\frac{1}{2}\log_2\left|x\right|=25\Leftrightarrow\log_2\left|x\right|=50\Leftrightarrow\left|x\right|=2^{50}\) Thỏa mãn
Vậy \(x=\pm2^{50}\) là nghiệm của phương trình
c) Điều kiện x>0. Phương trình đã cho tương đương với :
\(x^{lg^2x^2-3lgx-\frac{9}{2}}=\left(10^{lgx}\right)^{-2}\)
\(\Leftrightarrow lg^2x^2-3lgx-\frac{9}{2}=-2\)
\(\Leftrightarrow8lg^2x-6lgx-5=0\)
Đặt \(t=lgx\left(t\in R\right)\) thì phương trình trở thành
\(8t^2-6t-5=0\) hay\(t=-\frac{1}{2}\) V \(t=\frac{5}{4}\)
Với \(t=-\frac{1}{2}\) thì \(lgx=-\frac{1}{2}\Leftrightarrow x=\frac{1}{\sqrt{10}}\)
Với \(t=\frac{5}{4}\) thì \(lgx=\frac{5}{4}\Leftrightarrow x=\sqrt[4]{10^5}\)
Vậy phương trình đã cho có nghiệm \(x=\sqrt[4]{10^5}\) và \(x=\frac{1}{\sqrt{10}}\)



Đáp án : C.