Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\Rightarrow n\inƯ\left(5\right)=\left\{1;5\right\}\\ b,\Rightarrow n\inƯ\left(4\right)=\left\{1;2;4\right\}\\ c,\Rightarrow n\inƯ\left(27\right)=\left\{1;3\right\}\left(n< 7\right)\)

a: Gọi d=UCLN(4n+8;2n+3)
\(\Leftrightarrow4n+8-4n-6⋮d\)
\(\Leftrightarrow2⋮d\)
mà 2n+3 là số lẻ
nên d=1
=>ĐPCM
b: Gọi a=UCLN(7n+4;9n+5)
\(\Leftrightarrow63n+36-63n-35⋮a\)
=>a=1
=>ĐPCM

a) \(\frac{7n+8}{n}=\frac{7n}{n}+\frac{8}{n}=7+\frac{8}{n}\)
\(\Rightarrow n\in\text{Ư}\left(8\right)=\left\{1;2;4;8\right\}\)
b) \(\frac{35-12n}{n}=\frac{35}{n}-\frac{12n}{n}=\frac{35}{n}-12\)
\(\Rightarrow n\in\text{Ư}\left(35\right)=\left\{1;3;5;7;35\right\}\)
Loại \(n\in\left\{1;3\right\}\) vì n > 3.
Vậy: \(n\in\left\{5;7;35\right\}\)
c) \(\frac{n+8}{n+3}=\frac{n+3+5}{n+3}=\frac{n+3}{n+3}+\frac{5}{n+3}=1+\frac{5}{n+3}\)
\(\Rightarrow n+3\in\text{Ư}\left(5\right)=\left\{1;5\right\}\)
\(\Rightarrow n+3=1\Rightarrow n=1-3=-2\) (loại vì -2 < 0)
\(\Rightarrow n+3=5\Rightarrow n=2\)
Vậy: n = 2
giải đầy đủ ba câu nhưng không yêu cầu chi tiết
a. n phải chia hết cho n rồi cãi sao đuọc
7 n càng chia hết cho n
vậy 8 phải chia hết cho n
n=(1.2.4.8)
b. ồ n<3 thì còn mỗi 1.2 n=1 hiển nhiên rồi, n=2 ko cần tử biết loại
vậy n=1 (người ra câu nàylãng xẹt)
c. (n+8)/(n+3) ko có dấu chia hết tạm dùng (...) là dấu chia hết
(n+3) (...) (n+3) hiển nhiên
(n+8) (...) (n+3)
=>[n+8-(n+3)] (...)(n+3)
5(...)(n+3)
vậy n+3=(1,5)
n=(2)

n + 5 ) chia hết cho n ( n khác 0)
( 7n + 8) chia hết cho n ( n khác 0)
35 - 12n chia hết cho n ( n<3 và n khác 0)
a)\(\left(n+5\right)⋮n\)
\(\Rightarrow n+5=1;-1;5;-5\)
\(\Rightarrow n=-4;-6;0;-10\)

Bài 5:
b: Ta có: \(n+6⋮n+2\)
\(\Leftrightarrow n+2\in\left\{2;4\right\}\)
hay \(n\in\left\{0;2\right\}\)
c: Ta có: \(3n+1⋮n-2\)
\(\Leftrightarrow n-2\in\left\{-1;1;7\right\}\)
hay \(n\in\left\{1;3;9\right\}\)

a, Vì (n+3) ⋮ (n+3) nên để (n+8) ⋮ (n+3) thì: [(n+8) - (n+3)] ⋮ (n+3) hay 5 ⋮ (n+3), Suy ra: n+3 ∈ {1;5}
Vì n + 3 ≥ 3 nên n + 3 = 5 => n = 2
Vậy n = 2
b, Vì 3(n+4) ⋮ (n+4) nên để (16 - 3n) ⋮ (n+4) thì: [(16 - 3n)+3(n+4)] ⋮ (n+4) hay 28 ⋮ (n+4)
Suy ra: n+4 ∈ {1;2;4;7;14;28}
Vì 0 ≤ n ≤6 nên 4 ≤ n+4 ≤ 10.
Từ đó ta có: n+4 ∈ {4;7} hay n ∈ {0;3}
c, Vì 5(9 - 2n) ⋮ (9 - 2n) nên nếu (5n+2) ⋮ (9 - 2n) thì 2(5n+2) ⋮ (9 - 2n)
Suy ra: [5(9 - 2n)+2(5n+2)] ⋮ (9 - 2n) hay 49 ⋮ (9 - 2n) => 9 - 2n ∈ {1;7;49}
Vì 9 - 2n ≤ 9 nên 9 - 2n ∈ {1;7}
Từ đó ta có n ∈ {4;1} với n < 5
Thử lại ta thấy n = 4 hoặc n = 1 đều thõa mãn.
Vậy n ∈ {4;1}
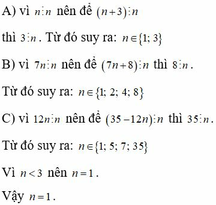
a, Vì n ⋮ n nên để (n+3) ⋮ n thì 3 ⋮ n. Từ đó suy ra: n ∈ {1;3}
b, Vì 7n ⋮ n nên để (7n+8) ⋮ n thì 8 ⋮ n. Từ đó suy ra: n ∈ {1;2;4;8}
c, Vì 12n ⋮ n nên để (35 - 12n) ⋮ n thì 35 ⋮ n. Từ đó suy ra: n ∈ {1;5;7;35}
Vì n < 3 nên n = 1
Vậy n = 1
(n+3):3