
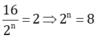
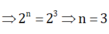
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

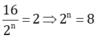
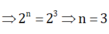

a. \(4^{15}.9^{15}< 2^n.3^n< 18^{16}.2^{16}\)
\(\Rightarrow2^{30}.3^{30}< 2^n.3^n< \left(3^2\right)^{16}.2^{16}.2^{16}\)
\(\Rightarrow2^{30}.3^{30}< 2^n.3^n< 3^{32}.2^{32}\)
\(\Rightarrow30< n< 32\)
\(\Rightarrow n=31\)
Vậy : \(n=31\)
\(n=0\Rightarrow b=3\)
Với \(n\ne0\Rightarrow VP⋮2butVT\) ko chia hết cho 2 nên ko thỏa mãn
Vậy \(n=0;b=3\)

\(a,\frac{16}{2^n}=2\Rightarrow2^n=16:2\Rightarrow2^n=8\Rightarrow2^n=2^3\Rightarrow n=3\)
\(b,\frac{\left(-3\right)^n}{81}=-27\Rightarrow\left(-3\right)^n=81.\left(-27\right)\Rightarrow\left(-3\right)^n=-2187\Rightarrow3^n=3^7\Rightarrow n=7\)
\(c,8^n:2^n=4\Rightarrow4^n=4\Rightarrow n=1\)
\(a,\frac{16}{2^n}=2\) \(b,\frac{\left(-3\right)^n}{81}=-27\) \(c,8^n:2^n=4\)
\(\Rightarrow2^4=2^n.2\) \(\Rightarrow\left(-3\right)^n=\left(-27\right).81\) \(\Rightarrow\left(8:2\right)^n=4\)
\(\Rightarrow4=n+1\) \(\Rightarrow\left(-3\right)^n=\left(-3\right)^7\) \(\Rightarrow4^n=4\)
\(\Rightarrow n=4-1=3\) \(\Rightarrow n=7\) \(\Rightarrow n=1\)
Tìm số tự nhiên n, biết:
a) \(\frac{16}{2^n}=2\)
b) \(\frac{\left(-3\right)^n}{81}=-27\)
c) \(8^n:2^2\)

a) \(\frac{16}{2^n}=2\)
=> 16 = 2 . 2n
=> 16 = 2n+1
=> 24 = 2n+1
=> n + 1 = 4
=> n = 4 - 1
=> n = 3
Vậy n = 3
b) \(\frac{\left(-3\right)^n}{81}=-27\)
=> (-3)n = -27 . 81
=> (-3)n = (-3)3 . (-3)4
=> (-3)n = (-3)7
=> n = 7
Vậy n = 7
c) 8n : 22 = bao nhiêu vậy ban?
Chuk bn hk tốt!![]()
a)\(\frac{16}{2^n}=2\)
\(\Rightarrow16:2=2^n\)
2n=8=23
Vậy n=3
b)\(\frac{\left(-3\right)^n}{81}=-27\)
\(\Rightarrow\)(-3)n=-27.81
(-3)n=-2187=(-3)7
Vậy n=7
c)Mk ko hiểu bn ghi gì

a) 162n=2 => \(\dfrac{2^4}{2^n}=2\Rightarrow2^{4-n}=2\Rightarrow4-n=1\Rightarrow n=3\)
b,
\(\dfrac{\left(-3\right)^n}{81}=-27\Rightarrow\dfrac{\left(-3\right)^n}{\left(-3\right)^4}=-27\Rightarrow\left(-3\right)^{n-4}=\left(-3\right)^3\Rightarrow n-4=3\Rightarrow n=7\)
c,\(8^n:2^n=4\Rightarrow4^n=4\Rightarrow n=1\)
 => (-3)n-4 = (-3)3
=> (-3)n-4 = (-3)3
=> n - 4 = 3 => n = 7
c) 8n : 2n = 4
4n = 4.

a)
\(\frac{16}{2^x}=2\)
\(\Rightarrow2^{x+1}=16\)
\(\Rightarrow2^{x+1}=2^4\)
\(\Rightarrow x+1=4\)
\(\Rightarrow x=3\)
b)
\(\frac{\left(-3\right)^x}{81}=-27\)
\(\Rightarrow\left(-3\right)^x=-\left(3^3.3^4\right)\)
\(\Rightarrow-3^x=-3^7\)
=> x=7
c)
\(8^n:2^n=4\)
\(\Rightarrow2^{3n}:2^n=4\)
\(\Rightarrow2^{3n-n}=4\)
\(\Rightarrow2^{2n}=2^2\)
=>2n=2
=>n=1
a)\(\frac{16}{2^n}=2\)
=>16:2n=2
=>2n=16:2
=>2n=8
b)ko nhớ cách làm
c)8n:2n=4
=>(23)n:2n=22
=>23n:2n=22
=>23n-n=22
=>22n=22
=>2n=2
=>n=1
dc rùi chứ


\(\frac{16}{2^n}=1;2^n=8;n=3\)
\(\frac{\left(-3\right)^n}{81}=-27;\left(-3\right)^n=\left(-3\right)^7;n=7\)
\(8^n:2^n=4;\left(8:2\right)^n=4;4^n=4=4^1;n=1\)

a, \(\frac{16}{2^n}=2\Leftrightarrow2\cdot2^n=16\Leftrightarrow2^{n+1}=2^4\Leftrightarrow n+1=4\Rightarrow n=3\)
b,\(\frac{\left(-3\right)^n}{81}=-27\Leftrightarrow\left(-3\right)^n=-3^3.3^4\Leftrightarrow\left(-3\right)^n=\left(-3\right)^7\Rightarrow n=7\)
c,\(8^n:2^n=4\Leftrightarrow\left(2^3\right)^n:2^n=2^2\Leftrightarrow2^{3n}:2^{2n}=2^2\Leftrightarrow2^{3n-2n}=2^2\Leftrightarrow2^n=2^2\Leftrightarrow n=2\)
câu 1. \(\frac{16}{2^n}\)=2 =>2n=16x2=32
2n=25 => n=5
câu 2.\(\frac{\left(-3\right)^n}{81}\)=-27=33 =>(-3)n =81x33
=(-3)4x(-3)3
=(-3)7
câu 3. 8n:4n=4=>(8:4)n=4
2n=4 =22
=>n=2

Ta có : \(2^m+2^n=2^{m+n}\)
\(\Leftrightarrow\frac{2^m+2^n}{2^{m+n}}=1\)
\(\Leftrightarrow\frac{1}{2^n}+\frac{1}{2^m}=1\)
+) Xét \(m=0\Rightarrow\frac{1}{2^0}+\frac{1}{2^n}>1\) ( loại )
+) Xét \(m=1\Rightarrow\frac{1}{2^m}=\frac{1}{2}\Rightarrow n=1\) ( thỏa mãn)
+) Xét \(m>1\Rightarrow\frac{1}{2^m}< \frac{1}{2},\frac{1}{2^n}< \frac{1}{2}\Rightarrow\frac{1}{2^m}+\frac{1}{2^n}< 1\) ( Do n là số tự nhiên, loại )
Vậy : \(m=1,n=1\) thỏa mãn đề.
\(2^m+2^n=2^{m+n}\)\(\Leftrightarrow2^{m+n}-\left(2^m+2^n\right)=0\)
\(\Leftrightarrow2^{m+n}-2^m-2^n=0\)\(\Leftrightarrow\left(2^{m+n}-2^m\right)-2^n+1=1\)
\(\Leftrightarrow2^m\left(2^n-1\right)-\left(2^n-1\right)=1\)\(\Leftrightarrow\left(2^m-1\right)\left(2^n-1\right)=1\)
Vì m , n là số tự nhiên \(\Rightarrow2^m-1\)và \(2^n-1\)cũng là số tự nhiên
\(\Rightarrow\hept{\begin{cases}2^m-1=1\\2^n-1=1\end{cases}}\Leftrightarrow\hept{\begin{cases}2^m=2\\2^n=2\end{cases}}\Leftrightarrow m=n=1\)
Vậy \(m=n=1\)