Tìm số tự nhiên a, biết rằng:a) a là số nhỏ nhất khác 0 thỏa mãn a ⋮ 15 và a ⋮ 115 b)...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

10 tháng 9 2018

Tìm số tự nhiên a, biết rằng:

a) a là số nhỏ nhất khác 0 thỏa mãn a ⋮ 15 và a ⋮ 115

b) a - 1 ⋮ 52 , a - 1 ⋮ 35 và 1000 < a < 2000

#Toán lớp 6

Cao Minh Tâm

10 tháng 9 2018

Đúng(2)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

4 tháng 10 2019

Tìm số tự nhiên a, biết rằng:a, a là số nhỏ nhất khác 0 thỏa mãn a chia hết cho 15 và 115b, a – 1 chia hết cho 52; a – 1 chia hết cho 35 và 1000 < a <...

Đọc tiếp

#Toán lớp 6

Cao Minh Tâm

4 tháng 10 2019

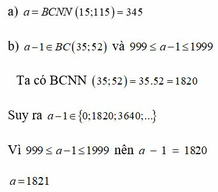
a, a = BCNN(15;115) = 345

b, a – 1 ∈ BC(35;52) và 999 < a – 1 < 1999

Ta có BCNN(35;52) = 35.52 = 1820

Suy ra a – 1 ∈ {0;1820;3640;...}

Vì 999 < a – 1 < 1999 nên a – 1 = 1820

a = 1821

Đúng(0)

Pham Trong Bach

20 tháng 2 2018

Tìm các số tự nhiên x biết:a) x ⋮ 15 , x ⋮ 35 , x ⋮ 42 và 250 < x < 850 .b) x là số nhỏ nhất khác 0 thoả mãn x ⋮ 15 v à x ⋮ 115 c) x - 1 ⋮ 52 , x - 1 ⋮ 35 và 1000 < x < 2000 ...

Đọc tiếp

#Toán lớp 6

Cao Minh Tâm

20 tháng 2 2018

Đúng(0)

Lê Anh Thư

8 tháng 8 2023 - olm

Bài 2. Tìm các số tự nhiên x biết:
a) x:15, x:35, x:42 và 250 < x < 850 .
b) x là số nhỏ nhất khác 0 thoả mãn x:15 và x:115;
c) (x−1)52,(x−1) 35 và 1000 < x < 2000

#Toán lớp 6

Nguyễn Đức Trí

8 tháng 8 2023

a) \(x⋮15;x⋮35;x⋮42\&250< x< 850\) (sửa dấu chia thành chia hết)

\(BCNN\left(15;35;42\right)=210\)

\(\Rightarrow x\in BC\left(15;35;42\right)=\left\{0;210;420;630;840;...\right\}\)

mà \(250< x< 850\)

\(\Rightarrow x\in\left\{420;630;840\right\}\)

b) x nhỏ nhất khác 0 thỏa mãn \(x⋮15;x⋮115\)

\(BCNN\left(15;115\right)=345\)

Vậy \(x\in\left\{345\right\}\) thỏa mãn đề bài

Đúng(1)

Nguyễn Đức Trí

8 tháng 8 2023

Bài c bạn xem lại đề

Đúng(0)

Trần Hồng

25 tháng 12 2022

Số tự nhiên a lớn nhất thỏa mãn 75 ⋮ a và 100 ⋮ a là:

Số tự nhiên a nhỏ nhất thỏa mãn 20 ⋮ a và 35 ⋮ a là:

#Toán lớp 6

Slime

25 tháng 12 2022

1: a = 25

2 : a = 1

Đúng(0)

Nguyễn Vũ Gia An

25 tháng 12 2022

1.a= 25

2.a=5

Đúng(0)

hoangngocphuong

6 tháng 11 2015 - olm

Tìm số tự nhiên a nhỏ nhất khác 0 biết a chia hết cho 21;a chia hết cho 35

Giải:Vì a là số tự nhiên nhỏ nhất khác 0,chia hết cho cả 21 và 35 nên a là bội chung nhỏ nhất(21;35)

Phân tích 21 và 35 ra thừa số nguyên tố

21=.........................

35=..............................

Bội chung nhỏ nhất(21;35)=

Vậy số a=......................

#Toán lớp 6

Minh Hiền

6 tháng 11 2015

21=3.7

35=5.7

BCNN(21,35)=3.5.7=105

Vậy a=105.

Đúng(0)

Trần Nguyễn Quốc Pháp

27 tháng 12 2021

đốt vừa thôi

Đúng(0)

Pham Trong Bach

28 tháng 5 2018

Số tự nhiên a nhỏ nhất khác 0 thỏa mãn a ⋮ 18 và a ⋮ 40

A. 360

B. 400

C. 458

D. 500

#Toán lớp 6

Cao Minh Tâm

28 tháng 5 2018

Đáp án là A

Vì a là số tự nhiên nhỏ nhất khác 0 thỏa mãn a ⋮ 18 và a ⋮ 40 nên a = BCNN (18, 40)

Ta có:

18 = 2. 3 2

40 = 2 3 .5

⇒ BCNN(18, 40) = 2 3 . 3 2 .5 = 360

Đúng(0)

lê trần uyên thy

3 tháng 12 2021

Câu 1. Một số tự nhiên a khác 0 nhỏ nhất thỏa mãn a⋮12 và a⋮36. Khi đó a là *

A. ƯC(12, 36).

B. BC(12, 36).

C. ƯCLN(12, 36).

D. BCNN(12, 36).

#Toán lớp 6

ILoveMath

3 tháng 12 2021

Đúng(1)

Minh Hồng

3 tháng 12 2021

Đúng(0)

Huong Candy

7 tháng 11 2017 - olm

Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a bội chung nhỏ nhất là 15 và a bội chung nhỏ nhất là 18

#Toán lớp 6

lyli

7 tháng 11 2017

tóm lại BCNNcủa a là 15 và 18

[gợi ý] chúc bạn học tốt

Đúng(0)

Pham Trong Bach

24 tháng 10 2019

Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a ⋮ 15 và a ⋮ 18 .

#Toán lớp 6

Cao Minh Tâm

24 tháng 10 2019

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP