Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn viết lại đề được ko? Ko hiểu \(\frac{x'+x}{x}\) với \(x\ne0\) là gì
Các câu dưới cũng có kí hiệu này, chắc bạn viết nhầm sang kí hiệu nào đó, nó cũng ko phải kí hiệu đạo hàm

a) f(x) liên tục tại x0 = -2
Vì \(\lim\limits_{x\rightarrow-2}f\left(x\right)=f\left(-2\right)=25\)
b) Có: \(\lim\limits_{x\rightarrow\frac{1}{2}}f\left(x\right)=\lim\limits_{x\rightarrow\frac{1}{2}}\frac{\left(2x-1\right)\left(2x+1\right)}{2x-1}=\lim\limits_{x\rightarrow\frac{1}{2}}\left(2x+1\right)=2\)
mà \(f\left(\frac{1}{2}\right)=3\)
=> \(\lim\limits_{x\rightarrow\frac{1}{2}}f\left(x\right)\ne f\left(\frac{1}{2}\right)\)
=> f(x) gián đoạn tại x0 = 1/2
c) \(\lim\limits_{x\rightarrow2-}f\left(x\right)=\lim\limits_{x\rightarrow2-}=\lim\limits_{x\rightarrow2-}\left(2x^2+x-1\right)=9\)
\(f\left(2\right)=3.2-5=1\)
Vì \(\lim\limits_{x\rightarrow2-}f\left(x\right)\ne f\left(2\right)\)
nên f(x) gián đoạn tại x0 = 2

Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) – f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.

a) Giả sử ∆x là số gia của số đối tại x0= 1. Ta có:
∆y = f(1 + ∆x) - f(1) = 7 + (1 + ∆x) - (1 + ∆x)2 - (7 + 1 - 12) = -(∆x)2 - ∆x ;
= - ∆x - 1 ;
=
(- ∆x - 1) = -1.
Vậy f'(1) = -1.
b) Giả sử ∆x là số gia của số đối tại x0= 2. Ta có:
∆y = f(2 + ∆x) - f(2) = (2 + ∆x)3 - 2(2 + ∆x) + 1 - (23 - 2.2 + 1) = (∆x)3 + 6(∆x)2 + 10∆x;
= (∆x)2 + 6∆x + 10;
=
[(∆x)2 + 6∆x + 10] = 10.
Vậy f'(2) = 10.

a) Ta có  = 22 +2.2 +4 = 12.
= 22 +2.2 +4 = 12.
Vì ![]() nên hàm số y = g(x) gián đoạn tại x0 = 2.
nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12

a) Giả sử ∆x là số gia của số đối tại x0 = 1. Ta có:
∆y = f(1 + ∆x) - f(1) = (1 + ∆x)2 + (1 + ∆x) - (12+ 1) = 3∆x + (∆x)2;
= 3 + ∆x;
=
(3 + ∆x) = 3.
Vậy f'(1) = 3.
b) Giả sử ∆x là số gia của số đối tại x0 = 2. Ta có:
∆y = f(2 + ∆x) - f(2) = -
= -
;
= -
;
=
-
= -
.
Vậy f'(2) = - .
c) Giả sử ∆x là số gia của số đối tại x0 = 0.Ta có:
∆y = f(∆x) - f(0) = - ( -1) =
;
=
;
=
= -2.
Vậy f'(0) = -2


a) ∆y = f(x0+∆x) - f(x0) = f(2) - f(1) = 23 - 13 = 7.
b) ∆y = f(x0+∆x) - f(x0) = f(0,9) - f(1) =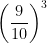 - 13 =
- 13 = 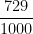 - 1 = -0,271.
- 1 = -0,271.