Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Điều kiện có sóng dừng trên dây hai đầu cố định l = kλ/2 (k là số bó sóng)
Cách giải: Ta có:
l = k λ 2 = 4 . v 2 f = 2 v f ⇒ v = lf 2 = 100 . 40 2 = 20 m / s .

+ Ta biễu diễn vị trí của M và N trên đường tròn.

Từ hình vẽ, ta thấy rằng có hai khả năng xảy ra của độ lệch pha


Đáp án D
Mức cường độ âm tại M: L M = 10 log I M I 0 ( d B ) = 10 log 10 - 8 10 - 12 = 40 ( d B )

Chọn đáp án A
@ Lời giải:
+ Sóng âm truyền từ môi trường không khí vào nước thì tần số không đổi.

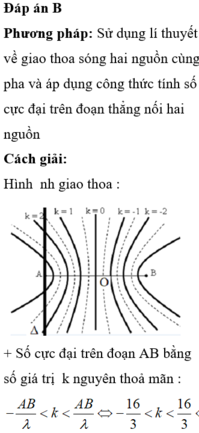
Đáp án B
Phương pháp: Phương trình giao thoa sóng trong giao thoa sóng hai nguồn cùng pha:
u M = 2 acos π ( d 2 - d 1 ) λ cos [ ωt - π ( d 2 + d 1 ) λ ]
Cách giải:
Bước sóng: λ = 2cm
Phương trình sóng tại M:
u M = 2 acos π ( MA - MB ) λ cos [ ωt - π ( MA + MB ) λ ]
X là điểm dao động với biên độ cực đại và ngược pha với M.
Phương trình sóng tại X:
u X = 2 acos π ( XA - XB ) λ cos [ ωt - π ( XA + XB ) λ ]
Vì X và M thuộc elip => M + MB = X + XB
=> uM và uX chỉ khác nhau về:
cos π ( MA - MB ) λ ; cos π ( XA - XB ) λ
Vì M thuộc trung trực của AB
⇒ cos π ( MA - MB ) λ = 1
X ngược pha với M
⇔ cos π ( XA - XB ) λ = - 1 ⇔ X A - X B = ( 2 k + 1 ) λ
- AB ≤ ( 2 k + 1 ) λ ≤ AB ⇔ - 19 ≤ ( 2 k + 1 ) λ ≤ 19 ⇒ - 5 , 25 ≤ k ≤ 4 , 25
=> Có 10 điểm dao động với biên độ cực đại và ngược pha với M trên đoạn B
=> Trên elip có 20 điểm dao động với biên độ cực đại và ngược pha với M.

Như ta biết, bản chất của giao thoa sóng là tổng hợp dao động do 2 nguồn truyền đến.
Do đó, dao động tại M là tổng hợp 2 dao động do A và B truyền đến.
Bước sóng: \(\lambda = 30/10 = 3cm\)
Độ lệch pha 2 dao động từ A, B truyền đến là: \(\Delta \varphi = 2\pi\frac{d_2-d_1}{\lambda}=2\pi\frac{13,5-10,5}{3}=2\pi\) (rad)
Biên độ tổng hợp: \(A_M=\sqrt{A_A^2+A_B^2+2A_AA_B\cos\Delta\varphi}=\sqrt{2^2+2^2+2.2.2.\cos2\pi}=4\)(cm)
Đáp án B



Chọn đáp án B
@ Lời giải:
+ Sóng âm không truyền được trong chân không, kể cả sóng siêu âm