NM
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 9 2021
a) \(4x+9=0\Leftrightarrow4x=-9\Leftrightarrow x=-\dfrac{9}{4}\)
b) \(-5x+6=0\Leftrightarrow5x=6\Leftrightarrow x=\dfrac{6}{5}\)
c) \(x^2-1=0\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
d) \(x^2-9=0\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
e) \(x^2-x=0\Leftrightarrow x\left(x-1\right)=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
f) \(x^2-2x=0\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
g) \(\left(x-4\right)\left(x^2+1\right)=0\Leftrightarrow x-4=0\Leftrightarrow x=4\)( do \(x^2+1\ge1>0\))
h) \(3x^2-4x=0\Leftrightarrow x\left(3x-4\right)=0\Leftrightarrow\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{4}{3}\end{matrix}\right.\)
i) \(x^2+9=0\Leftrightarrow x^2=-9\)( vô lý do \(x^2\ge0>-9\))
Vậy \(x\in\left\{\varnothing\right\}\)
1 tháng 3 2022
a: \(A=-5x^3+9x^3-2x^2-2x^2+x-x+1\)
\(=4x^3-4x^2+1\)
\(B=-4x^3+2x^3-2x^2+2x^2+6x-9x-2\)
\(=-2x^3-3x-2\)
\(C=x^3-6x^2+2x-4\)
b: \(A\left(x\right)+B\left(x\right)-C\left(x\right)\)
\(=4x^3-4x^2+1-2x^3-3x-2+x^3-6x^2+2x-4\)
\(=3x^3-10x^2-x-4\)
SP
2
ML
2
18 tháng 5 2021
a) \(\left(x-1\right)\left(x+5\right)=0\Rightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
b) \(x+1x^2+1=x^2+x+1=x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)với mọi x.
=> Pt vô nghiệm.
c) \(x^2+4x=0\Leftrightarrow x\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
P/s: Check lại đề ý b nhé.
18 tháng 5 2021
a) Ta có:(x-1)(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
Vậy: S={1;-5}
b) Ta có: \(x^2+x+1=0\)
\(\Leftrightarrow x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\)(Vô lý)
Vậy: \(S=\varnothing\)
c) Ta có: \(x^2+4x=0\)
\(\Leftrightarrow x\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Vậy: S={0;-4}
20 tháng 6 2023
8:
a: M(x)=x^4+2x^2+1
N(x)=x^4+2x^2-3x-14
P(x)=M(x)-N(x)=3x+15
P(x)=0
=>3x+15=0
=>x=-5
b: M(x)=x^2(x^2+1)+1>0
=>M(x) vô nghiệm
TT
18 tháng 4 2021
a/ \(M\left(x\right)=-x^2+5\)
Có \(-x^2\le0\forall x\)
=> \(M\left(x\right)\le5\forall x\)
=> M(x) không có nghiệm.
2/
Thay \(x=\dfrac{1}{2}\) vào đa thức M(x) có
\(M\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\)
\(\Leftrightarrow a=2\)
Vậy...
L
18 tháng 5 2022
a. M(x) + N(x) = 6x3 – 2x2 + 3x +10 - 6x3 + x2 – 6x -10
= (6x3 - 6x3 ) + ( -2x2 + x2 ) + ( 3x - 6x ) + ( 10 - 10 )
= -x2 - 3x
M(x) - N(x) = 6x3 – 2x2 + 3x +10 - ( –6x3 + x2 – 6x -10)
= 6x3 – 2x2 + 3x +10 + 6x3 - x2 + 6x +10
= (6x3 + 6x3 ) + ( -2x2 - x2 ) + ( 3x + 6x) + ( 10 + 10)
= 12x3 - 3x2 + 9x + 20
b. Đặt -x2 - 3x = 0
=> -x2 + (-3)x = 0
=> -x2 + 3.-x = 0
=> -x(-x+ 3) = 0
=>\(\left[{}\begin{matrix}-x=0\\-x+3=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\\-x=-3\end{matrix}\right.=>\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy nghiệm của đa thức trên là 0 hoặc -3
18 tháng 5 2022
a) M(X) + N(x)= (6x3 – 2x2 + 3x +10)
+ (–6x3 + x2 – 6x -10)
M(x) + N(x)= – x2 - 3x.
M(x) + N(x)= (6x3 – 2x2 + 3x +10)
- (–6x3 + x2 – 6x -10)
M(x) - N(x)= 12x3 - x2 + 9x + 20.
b) Nghiệm của M(x) + N(x)= x= 0, -3.
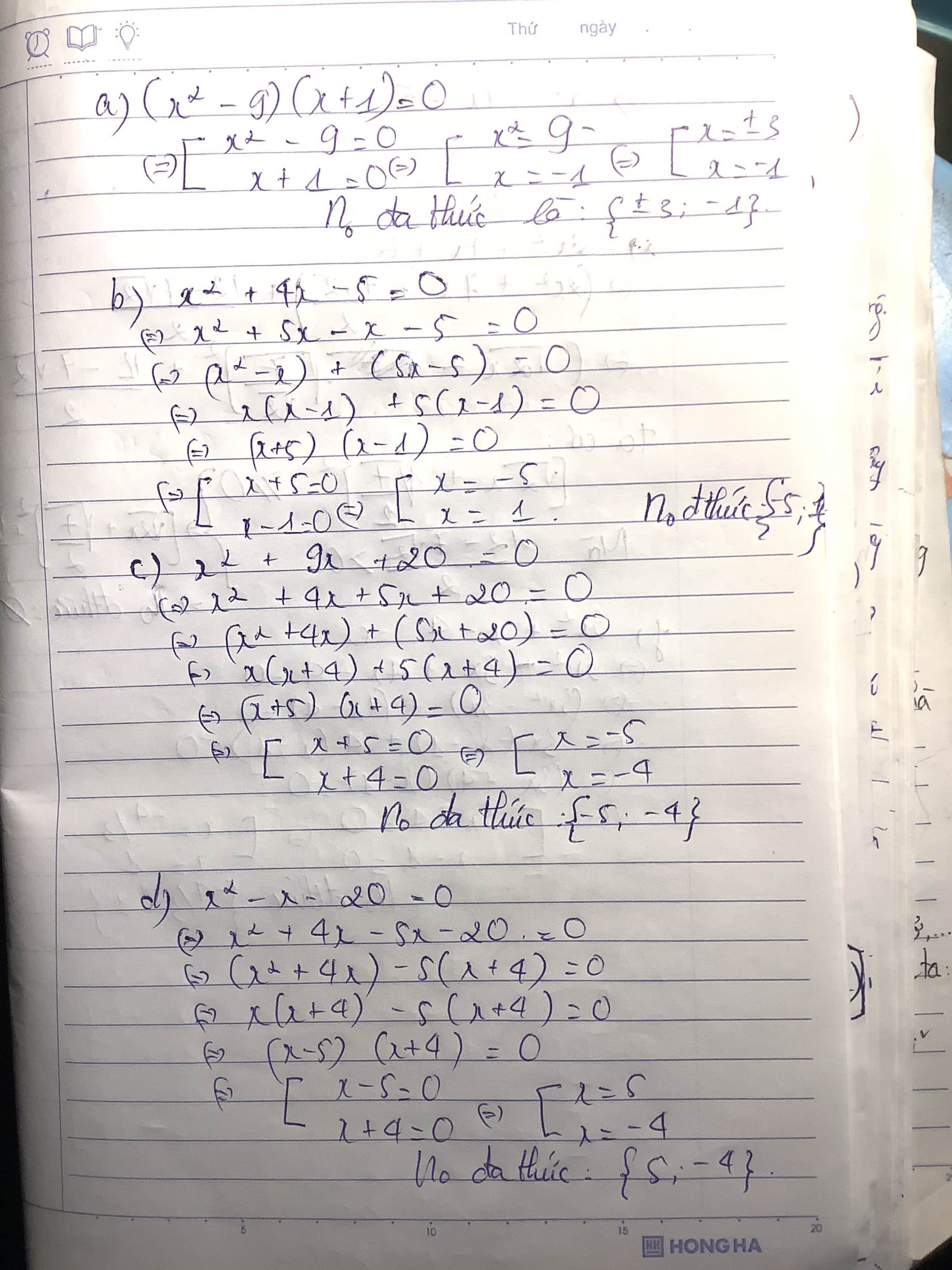
Nghiệm đa thức A là:
x2-6x=0 hoặc x2+5=0
x(x-6)=0 hoặc x2=-5 (mà x2 luôn dương nên trong TH này, không có giá trị x)
x=0 hoặc x-6=0
Vậy nghiệm của đa thức là 0 hoặc 6
Nghiệm đa thức A là:
x2-6x=0 hoặc x2+5=0
x(x-6)=0 hoặc x2=-5 (mà x2 luôn dương nên trong TH này, không có giá trị x)
x=0 hoặc x-6=0
Vậy nghiệm của đa thức là 0 hoặc 6