
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(z=x+yi\Rightarrow\sqrt{\left(x-3\right)^2+\left(y+4\right)^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow6x-8y-25=0\)
\(\Rightarrow y=\dfrac{6x-25}{8}\)
\(\Rightarrow\left|z\right|=\sqrt{x^2+\left(\dfrac{6x-25}{8}\right)^2}=\dfrac{5}{8}\sqrt{\left(2x-3\right)^2+16}\ge\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(x=\dfrac{3}{2};y=-2\Rightarrow z=\dfrac{3}{2}-2i\)
Không tồn tại \(\left|z\right|_{max}\)

Đặt a + bi(a, b ∈R). Ta có:
( 1 + 2 i ) 2 z = ( 1 + 2 i - 4 ) ( a + b i ) = - 3 a - 3 b i + 4 a i - 4 b = - 3 a - 4 b + ( 4 a - 3 b ) i
Do đó: ( 1 + 2 i ) 2 . z + a = 4 i - 20 <=> -3a - 4b + (4a - 3b)i + a - bi = 4i - 20
<=> -2a - 4b + (4a - 4b)i = 4i - 20
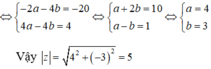
Chọn B
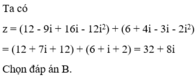
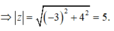
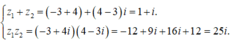
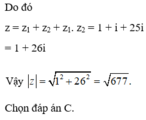
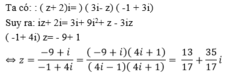

đặc \(z=a+bi\) (\(a;b\in R\) và \(i^2=-1\))
ta có : \(Y=3\left|z\right|+4\left|z-4i\right|+5\left|z-3\right|\)
\(\Leftrightarrow Y=3\left|a+bi\right|+4\left|a+\left(b-4\right)i\right|+5\left|\left(a-3\right)+bi\right|\)
\(\Leftrightarrow Y=3\sqrt{a^2+b^2}+4\sqrt{a^2+\left(b-4\right)^2}+5\sqrt{\left(a-3\right)^2+b^2}\)
áp dụng bất đẳng thức Bunhiacopxki ta có :
\(Y\ge-\sqrt{\left(3^2+4^2+5^2\right)\left(a^2+b^2+a^2+\left(b-4\right)^2+\left(a-3\right)^2+b^2\right)}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3a^2+3b^2-8b-6a+25}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3\left(a-1\right)^2+\left(\sqrt{3}b-\dfrac{8}{2\sqrt{3}}\right)^2+\dfrac{50}{3}}\)
dấu "=" xảy ra khi \(\dfrac{3}{\sqrt{a^2+b^2}}=\dfrac{4}{\sqrt{a^2+\left(b-4\right)^2}}=\dfrac{4}{\sqrt{\left(a-3\right)^2}+b^2}\)
giải ra tìm được \(a;b\) rồi thay ngược trở lại nha