Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Ta có: (z + 2)i = (3i - z)( -1 + 3i)
Suy ra: iz + 2i = 3i + 9i2 + z - 3iz
(-1 + 4i) z = - 9 + 1
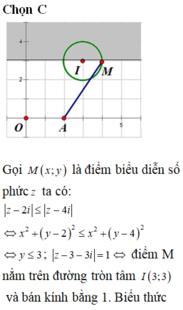
Chọn C.
Ta có |z|2 + |(z – 1 – 2i) + (1 + 2i)|2 = |z – 1- 2i|2 + |1 + 2i|2 + 2(z – 1 – 2i)(1 + 2i) (1)
|z – 3 – 6i|2 = |(z – 1 – 2i) – 2(1 + 2i)|2 = |z – 1 – 2i|2 + 4|1 + 2i|2 - 4(z – 1- 2i)(1 + 2i) (2)
Từ (1) và (2) suy ra: 2|z|2 + |z – 3- 6i|2 = 3|z – 1- 2i|2 + 6|1 + 2i| = 12 + 30 = 42.
Áp dụng bất đẳng thức Bunhiakovsky ta có:
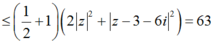
Vậy 
Đáp án D
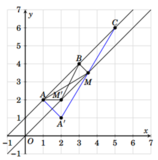
Cách 1
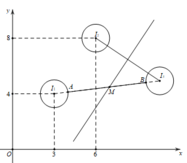
· Đặt 
biểu diễn cho số phức z.
· Từ giả thiết, ta có M thuộc đường trung trực 
của đoạn EF và P=AM+BM+CM
· Ta chứng minh điểm M chính là hình chiếu vuông góc của B lên đường thẳng ∆ .
- Với M’ tùy ý thuộc ∆ , M’ khác M. Gọi A’ là điểm đối xứng của A qua ∆ . Nhận thấy rằng ba điểm A’, M, C thẳng hàng.
- Ta có 
Mà 
Lại có 
Do đó 
Cách 2
· Gọi 
Từ giả thiết 
, dẫn đến y=x .
Khi đó z=x+xi.
· 
· Sử dụng bất đẳng thức 
Dấu đẳng thức xảy ra khi và chỉ khi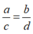 
. Ta có
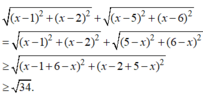
Dấu đẳng thức xảy ra khi và chỉ khi 
· Mặt khác
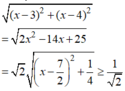
Dấu đẳng thức xảy ra khi và chỉ khi x= 7 2
· Từ hai trường hợp trên, ta thấy, giá trị nhỏ nhất của P là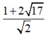 
.
Khi đó a+b=3.
Đáp án C
Phương pháp: Gọi 
là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
Lời giải chi tiết.
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng 
Khi đó ta có
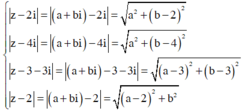
Từ giả thiết ta suy ra
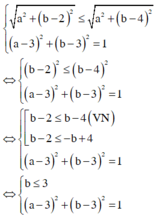
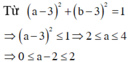
Do đó 
Đẳng thức xảy ra khi và chỉ khi
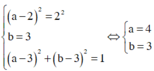
Chú ý. Đối với bài toán liên quan tới cực trị học sinh thường mắc phải sai lầm là quên tìm giá trị để cực trị xảy ra. Điều này có thể dẫn tới việc tìm sai giá trị lớn nhất nhỏ nhất
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng z = a+bi Khi đó ta có
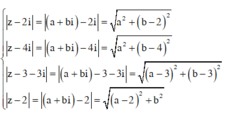
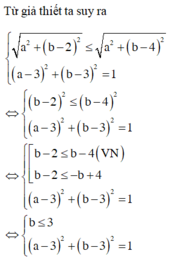
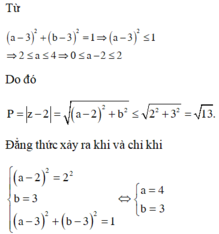
Đáp án C
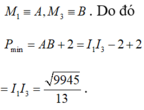
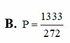
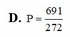
Chọn B.