Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
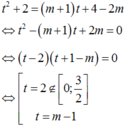
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.

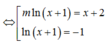
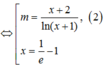

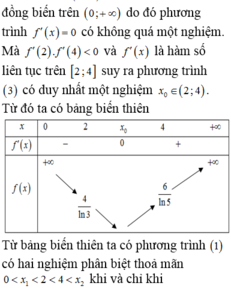
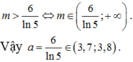



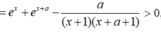
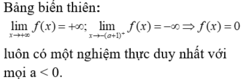


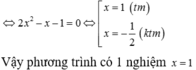
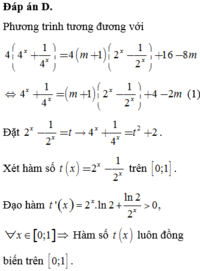


Lời giải:
Ta có:
\(m\ln (1-x)-\ln x=m\)
\(\Rightarrow m=\frac{\ln x}{\ln (1-x)-1}\)
Đặt \(f(x)=\frac{\ln x}{\ln (1-x)-1}\) \(\Rightarrow f'(x)=\frac{\frac{1}{x}(\ln (1-x)-1)+\frac{1}{1-x}.\ln x}{(\ln (1-x)-1)^2}\)
Với mọi \(x\in (0;1)\) thì \(\ln x< 0; \ln (1-x)< 0\).
\(\Rightarrow \frac{1}{x}(\ln (1-x)-1)+\frac{1}{1-x}.\ln x< 0\)
\(\Rightarrow f'(x)< 0, \forall x\in (0;1)\) hay hàm $f(x)$ nghịch biến trên $(0;1)$
-----------------
Lại có:
\(\lim _{x\to 0+}\frac{\ln x}{\ln (1-x)-1}=\lim_{x\to 0+}\frac{1}{\ln (1-x)-1}.\lim_{x\to +\infty}\ln x\)
\(-1.(-\infty)=+\infty\)
\(\lim_{x\to 1-}\frac{\ln x}{\ln (1-x)-1}=\lim _{x\to 1-}\ln x.\lim_{x\to 1-}\frac{1}{\ln (1-x)-1}=0.0=0\)
Do đó PT có nghiệm khi \(m\in (0;+\infty)\)