K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
0

LM
1
PT
tìm m để phương trình \(7x^3+\left(2m-9\right)x^2-\left(m^2+2m-2\right)x-2=0\) có 3 nghiệm phân biệt
0


CM
11 tháng 5 2017

Để phươmg trình đã cho có 2 nghiệm phân biệt nên pt (1) có hai nghiêm dương phân biệt
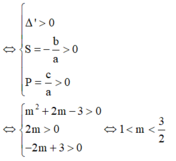
Chọn B




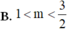
Lời giải:
PT $\Leftrightarrow mx^2-2x+3+2m=x+m$
$\Leftrightarrow mx^2-3x+(3+m)=0(*)$
Để pt ban đầu có 2 nghiệm trái dấu thì pt $(*)$ phải có 2 nghiệm trái dấu.
Điều này xảy ra khi \(\left\{\begin{matrix} m\neq 0\\ \Delta=9-4m(m+3)>0\\ \frac{3+m}{m}<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4m^2+12m-9<0\\ -3< m< 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{-3-3\sqrt{2}}{2}< m< \frac{-3+3\sqrt{2}}{2}\\ -3< m< 0\end{matrix}\right.\Leftrightarrow -3< m<0\)