Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(A=2x^3-9x^5+3x^5-3x^2+7x^2-12=-6x^5+2x^3+4x^2-12\)
b, \(B=2x^4+x^2+2x-2x^3-2x^2+x^2-2x+1=2x^4-2x^3+1\)
c, \(C=2x^2+x-x^3-2x^2+x^3-x+3=3\)

\(\left(ax^2+bx+c\right)\left(x+1\right)=ax^3+\left(a+b\right)x^2+\left(b+c\right)x+c\)
đồng nhất đa thức trên với đa thức đã cho ta được
\(\left\{{}\begin{matrix}a=1\\a+b=8\\b+c=19\\c=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=1\\b=7\\c=12\end{matrix}\right.\)
3 phần kia làm tương tự
b: \(\left(ax^2+bx+c\right)\left(x+3\right)\)
\(=ax^3+3ax^2+bx^2+3bx+cx+3c\)
\(=ax^3+x^2\left(3a+b\right)+x\left(3b+c\right)+3c\)
Theo đề, ta có:
\(\left\{{}\begin{matrix}3c=0\\3b+c=-3\\3a+b=2\\a=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=0\\b=-1\\a=1\end{matrix}\right.\)
c: \(\left(x^2+cx+2\right)\left(ax+b\right)\)
\(=a\cdot x^3+bx^2+ac\cdot x^2+bc\cdot x+2a\cdot x+2b\)
\(=a\cdot x^3+x^2\left(b+ac\right)+x\left(bc+2a\right)+2b\)
Theo đề, ta có: 2b=-2; bc+2a=0; b+ac=1; a=1
=>b=-1; a=1; c=2
d: \(\left(x^2+cx+1\right)\left(ax+b\right)\)
\(=a\cdot x^3+bx^2+ac\cdot x^2+bc\cdot x+a\cdot x+b\)
\(=a\cdot x^3+x^2\left(b+ac\right)+x\left(bc+a\right)+b\)
Theo đề, ta có:
b=2; bc+a=-3; b+ac=0; a=1
=>b=2; a=1; bc=-3-a=-3-1=-4
=>b=2; a=1; 2c=-4
=>b=2; a=1; c=-2

a: \(\left(x^2+cx+2\right)\left(ax+b\right)\)
\(=ax^3+bx^2+ac\cdot x^2+bc\cdot x+2ax+2b\)
\(=ax^3+x^2\left(b+ac\right)+x\left(bc+2a\right)+2b\)
Theo đề, ta có: a=1; 2b=-2; b+ac=1 và bc+2a=0
=>a=1; b=-1; c-1=1; bc+2a=0
=>a=1; b=-1; c=2
b: \(\left(x^2-x+1\right)\left(ax^2+bx+c\right)\)
\(=ax^4+bx^3+cx^2-ax^3-bx^2-cx+ax^2+bx+c\)
\(=ax^4+x^3\left(b-a\right)+x^2\left(c-b+a\right)+x\left(-c+b\right)+c\)
Theo đề, ta có:
a=2; b-a=-1; c-b+a=2; -c+b=0; c=1
=>a=2; b=-1+a=-1+2=1; c=1
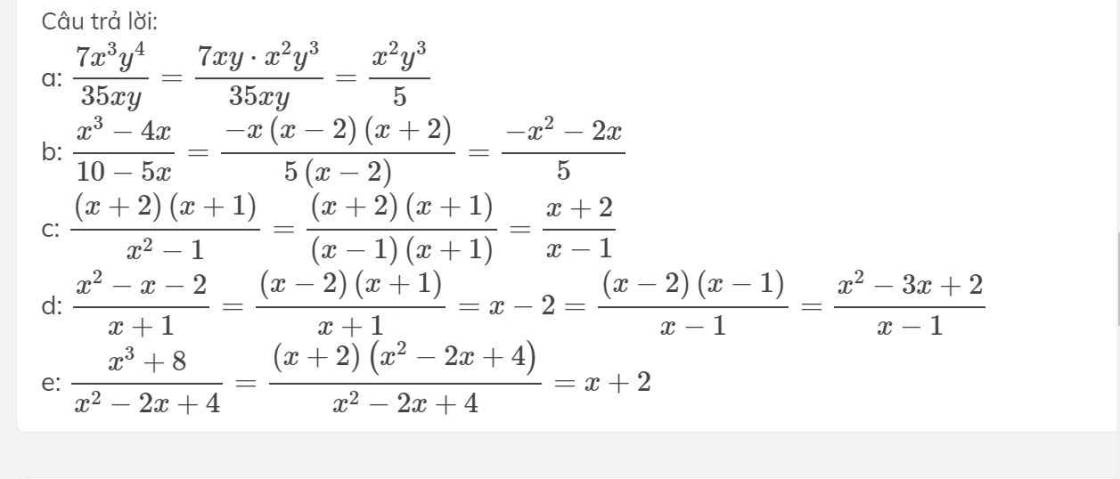
bạn ghi lại đề đi mình chả hiểu cái mô tê gì cả