K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 8 2019
GTNN cua A la khi 2x^2-8x=0
=>x=0=>GTNN cua A = 0-0+1=1
DF
1
AH
Akai Haruma
Giáo viên
2 tháng 1 2021
Bạn xem lại ĐKĐB. Nếu $x\geq \frac{-1}{3}$ thì mình nghi ngờ $\sqrt{3x-1}$ của bạn viết là $\sqrt{3x+1}$Còn nếu đúng là $\sqrt{3x-1}$ thì ĐK cần là $x\geq \frac{1}{3}$.
7 tháng 7 2016
\(B=5x^2+x+1\)
\(=>5\left(x^2+\frac{1}{5}x+\frac{1}{5}\right)\)
\(=>5\left(x^2+2.x.\frac{1}{10}+\frac{1}{100}+\frac{19}{100}\right)\)
\(=>5\left(\left(x+\frac{1}{10}\right)^2+\frac{19}{100}\right)\)
\(=>\frac{19}{20}+5\left(x+\frac{1}{10}\right)^2\ge\frac{19}{20}\)
MIN B = \(\frac{19}{20}< =>x+\frac{1}{10}=0=>x=\frac{-1}{10}\)
NV
7 tháng 7 2016
B = 5x2 + x - 1
\(=5\left(x^2+\frac{1}{5}x-\frac{1}{5}\right)=5\left[x^2+2.\frac{1}{10}.x+\left(\frac{1}{10}\right)^2-\left(\frac{1}{10}\right)^2-\frac{1}{5}\right]\)
\(=5\left[\left(x+\frac{1}{10}\right)^2-\frac{21}{100}\right]=5\left(x+\frac{1}{10}\right)^2-\frac{21}{20}\ge-\frac{21}{20}\)
Vậy MinB = -21/20 khi \(x+\frac{1}{10}=0\Rightarrow x=-\frac{1}{10}\)
N
1
20 tháng 10 2021
Bài 2:
a: Ta có: \(x^2+4x+7\)
\(=x^2+4x+4+3\)
\(=\left(x+2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi x=-2
PT
1
29 tháng 9 2019
Đặt
\(A=4x^2-4x+1+25x^2+10x+1\)
\(A=29x^2+6x+2\)
\(A=29\left(x^2-\frac{6}{29}x+\frac{9}{841}\right)+\frac{49}{29}\)
\(A=29\left(x-\frac{3}{9}\right)^2+\frac{49}{29}\ge\frac{49}{29}\)
\(A_{min}=\frac{49}{29}\) khi \(x=\frac{3}{29}\)
Chúc bạn học tốt !!!
MA
1
23 tháng 10 2023
x+y=1
=>x=1-y
M=5x^2+y^2
=5(1-y)^2+y^2
\(=5y^2-10y+5+y^2\)
\(=6y^2-10y+5\)
\(=6\left(y^2-\dfrac{5}{3}y+\dfrac{5}{6}\right)\)
\(=6\left(y^2-2\cdot y\cdot\dfrac{5}{6}+\dfrac{25}{36}+\dfrac{5}{36}\right)\)
\(=6\left(y-\dfrac{5}{6}\right)^2+\dfrac{5}{6}>=\dfrac{5}{6}\)
Dấu = xảy ra khi y=5/6
=>\(M_{min}=\dfrac{5}{6}\) khi y=5/6 và x=1/6
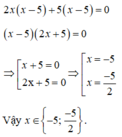
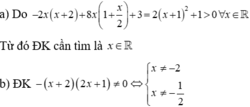
Ta có: \(2x^2-5x+1=\left(\sqrt{2}x\right)^2-2.\sqrt{2}x.\frac{5}{2\sqrt{2}}+\frac{25}{8}-\frac{17}{8}\)
\(=\left(\sqrt{2}x-\frac{5}{2\sqrt{2}}\right)^2-\frac{17}{8}\ge-\frac{17}{8}\)
(Dấu "="\(\Leftrightarrow\sqrt{2}x-\frac{5}{2\sqrt{2}}=0\Leftrightarrow x=\frac{5}{4}\))