K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 9 2021
\(\left|x-\dfrac{2}{3}\right|-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)
GB
1
KV
20 tháng 3 2023
A = 5x² + 6
Do x² ≥ 0
⇒ 5x² ≥ 0
⇒ 5x² + 6 ≥ 6
Vậy giá trị nhỏ nhất của A là 6 khi x = 0
--------------------
B = 4(2x - 4)² + 2023
Do (2x - 4)² ≥ 0
⇒ 4(2x - 4)² ≥ 0
⇒ 4(2x - 4)² + 2023 ≥ 2023
Vậy giá trị nhỏ nhất của B là 2023 khi x = 2
1 tháng 11 2017
a, A=15-|x+1|
Co: |x+1|> hoac = 0 voi moi x.
=>15-|x+1|< hoac = 15 vs moi x.
MAX A=15 khi |x+1|=0
=>x+1=0
x=-1.
b,Co: |x-2|> hoac bang 0.
=>18+|x-2|> hoac bang 18.
Min B=18 khi |x+2|=0
=>x+2=0
x=-2
Nho k cho mk nhe
LH
3
T
24 tháng 11 2016
Ta có: (2x+1)^2 lớn hơn hoặc bằng 0 suy ra (2x+1)^2+4 lớn hơn hoặc bằng 0 suy ra căn (2x+1)+4 lớn hơn hoặc bằng 0
Lại có:|4y^2-1|lớn hơn hoặc bằng 0 suy ra 3.|4y^2-1| lớn hơn hoặc bằng 0
nên GTNN của A =5 khi và chỉ khi (2x+1)^2+4=0 và 4y^2-1=0
Với (2x-1)^2-4=0 suy ra (2x+1)^2=-4 suy ra 2x+2= -2 hoặc 2. Nếu 2x+1=-2 suy ra x=-3/2; nếu 2x+1=2 thì x=1/2
Với 4y^2-1=0 suy ra 4y^2=1 suy ra y^2=1/4 suy ra y=1/2 và y=-1/2
24 tháng 11 2016
giá trị nhỏ nhất là 10 đạt đc khi x = 0,5 và y = 0
g
CC
1
AH
Akai Haruma
Giáo viên
31 tháng 7
Lời giải:
$x-y=2\Rightarrow x=y+2$
$C=|x+1|+|2y+1|=|y+2+1|+|2y+1|=|y+3|+|2y+1|$
Nếu $y\geq \frac{-1}{2}$ thì:
$C=y+3+2y+1=4y+4\geq 4.\frac{-1}{2}+4=2$
Nếu $\frac{-1}{2}> y\geq -3$ thì:
$C=y+3+[-(2y+1)]=2-y> 2-\frac{-1}{2}=2,5$
Nếu $y< -3$ thì:
$C=-y-3-2y-1=-4y-4=-4(y+1)> -4(-3+1)=8$
Từ các TH trên suy ra $C_{\min}=2$ khi $y\geq \frac{-1}{2}$
HT
3
S
1 tháng 10 2017
D = |x - 2| + |x - 3| + |x - 4| = (|x - 2| + |4 - x|) + |x - 3|
Ta có: \(\left|x-2\right|+\left|4-x\right|\ge\left|x-2+4-x\right|=2\)
Mà \(\left|x-3\right|\ge0\)
\(\Rightarrow D\ge2\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left(x-2\right)\left(4-x\right)\ge0\\x-3=0\end{cases}\Rightarrow\hept{\begin{cases}2\le x\le4\\x=3\end{cases}\Rightarrow}x=3}\)
Vậy MaxD = 2 khi x = 3
15 tháng 9 2016
T/C của gttđ là >= 0 nên
a) GTNN = -4
b) GTLN = 2
c) GTNN = 2
NC
13 tháng 8 2020
Bài làm:
a) Ta có: \(A=\left|x-\frac{3}{4}\right|\ge0\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\left|x-\frac{3}{4}\right|=0\Rightarrow x=\frac{3}{4}\)
Vậy Min(A) = 0 khi x=3/4
b) Ta có: \(B=-\left|x+2020\right|\le0\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\left|x+2020\right|=0\Rightarrow x=-2020\)
Vậy Max(B) = 0 khi x = -2020
13 tháng 8 2020
A = | x - 3/4 |
\(\left|x-\frac{3}{4}\right|\ge0\forall x\Rightarrow A\ge0\)
Dấu " = " xảy ra <=> x - 3/4 = 0 => x = 3/4
Vậy AMin = 0 , đạt được khi x = 3/4
B = - | x + 2020 |
\(\left|x+2020\right|\ge0\forall x\Rightarrow-\left|x+2020\right|\le0\forall x\)
\(\Rightarrow B\le0\)
Dấu " = " xảy ra <=> x + 2020 = 0 => x = -2020
Vậy BMax = 0, đạt được khi x = -2020
W
0
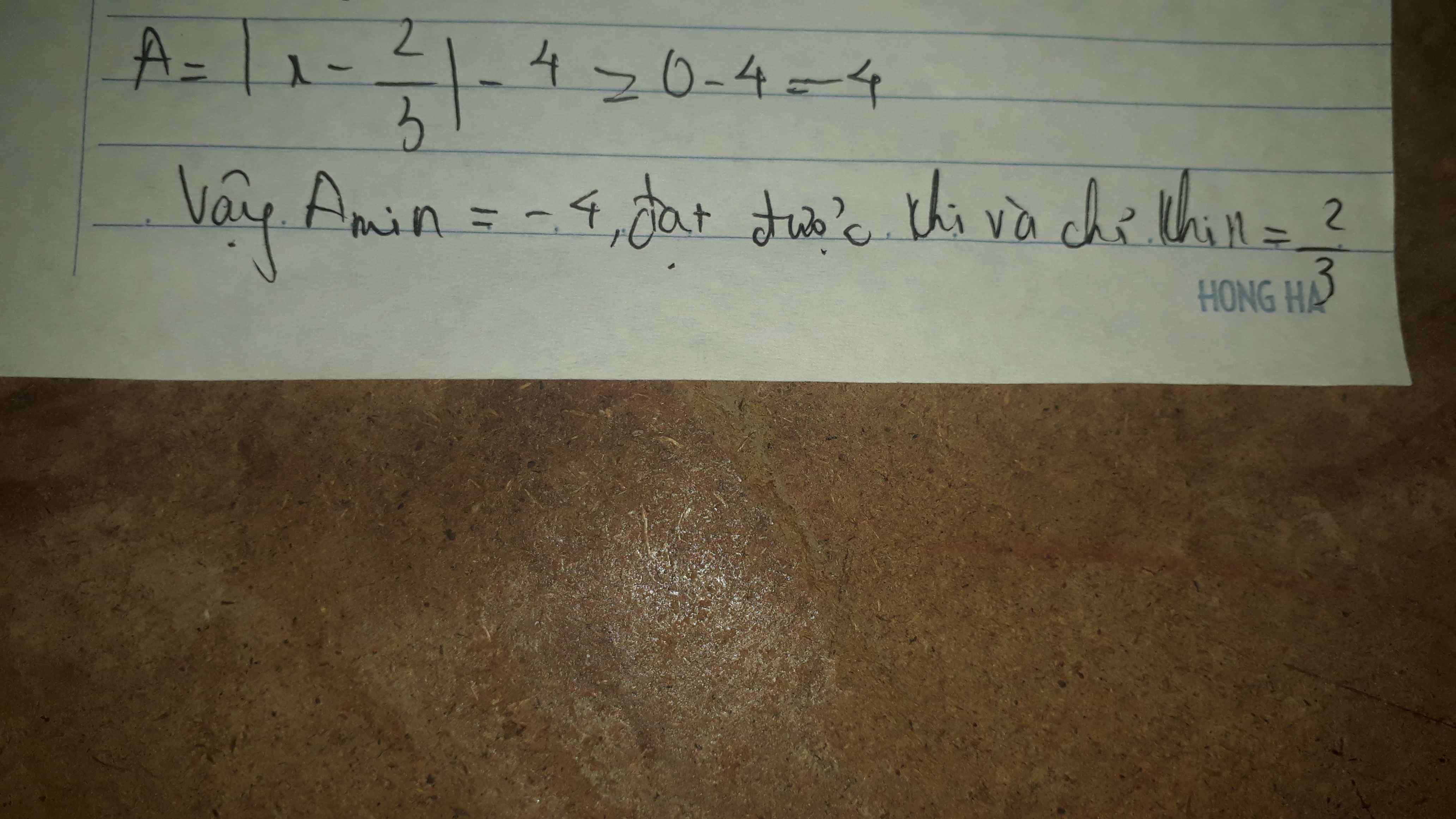
\(A=\left|x-\frac{1}{2}\right|-\frac{3}{4}\)
Vì \(\left|x-\frac{1}{2}\right|\ge0\forall x\)
\(\Rightarrow\left|x-\frac{1}{2}\right|-\frac{3}{4}\ge-\frac{3}{4}\forall x\)
\(\Rightarrow A_{min}=-\frac{3}{4}\Leftrightarrow\left|x-\frac{1}{2}\right|=0\Leftrightarrow x=\frac{1}{2}\)
\(A=\left|x-\frac{1}{2}\right|-\frac{3}{4}\ge-\frac{3}{4}\)
Dấu ''='' xảy ra khi x = 1/2
Vậy GTNN của A bằng -3/4 tại x = 1/2