Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1-cos^2x+1-cos^2y=\frac{1}{4}\Rightarrow cos^2x+cos^2y=\frac{7}{4}\)
\(\Rightarrow\frac{3}{4}\le cos^2x;cos^2y\le1\)
\(S=1+tan^2x+1+tan^2y-2=\frac{1}{cos^2x}+\frac{1}{cos^2y}-2\)
\(=\frac{7}{4cos^2x.cos^2y}-2=\frac{7}{4cos^2x\left(\frac{7}{4}-cos^2x\right)}-2=\frac{7}{-4cos^4x+7cos^2x}-2\)
Đặt \(cos^2x=t\) \(\Rightarrow\frac{3}{4}\le t\le1\)
Xét \(f\left(t\right)=-4t^2+7t\) trên \(\left[\frac{3}{4};1\right]\)
\(-\frac{b}{2a}=\frac{7}{8}\Rightarrow f\left(\frac{7}{8}\right)=\frac{49}{16}\) ; \(f\left(\frac{3}{4}\right)=3\); \(f\left(1\right)=3\)
\(\Rightarrow3\le f\left(t\right)\le\frac{49}{16}\)
\(\Rightarrow\frac{7}{\frac{49}{16}}-2\le S\le\frac{7}{3}-2\Leftrightarrow\frac{2}{7}\le S\le\frac{1}{3}\)
Không có trong đáp án?

1.
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\frac{\pi}{6}+k2\pi\\2x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{12}+k\pi\\x=\frac{7\pi}{12}+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\frac{7\pi}{12}\)
2.
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{3}+k2\pi\\2x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k\pi\\x=-\frac{\pi}{6}+k\pi\end{matrix}\right.\)
Nghiệm âm lớn nhất là \(x=-\frac{\pi}{6}\)

\(I\left(1;1\right)\) , bán kính \(R=2\)
Do \(sin\widehat{AIB}\le1\Rightarrow S_{IAB}=\frac{1}{2}IA.IB.sin\widehat{AIB}\le\frac{1}{2}IA.IB=\frac{1}{2}R^2=2\)
\(\Rightarrow S_{max}=2\) khi \(\widehat{AIB}=90^0\)
Gọi H là hình chiếu của I lên AB, áp dụng hệ thức lượng cho tam giác vuông AIB:
\(\frac{1}{IH^2}=\frac{1}{IA^2}+\frac{1}{IB^2}=\frac{2}{R^2}\Rightarrow IH=\frac{R}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow d\left(I;AB\right)=\sqrt{2}=\frac{\left|1+1-m\right|}{\sqrt{1^2+1^2}}\Rightarrow\left|2-m\right|=2\Rightarrow\left[{}\begin{matrix}m=0\\m=4\end{matrix}\right.\)
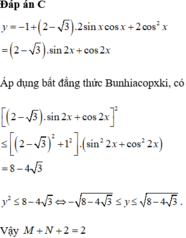

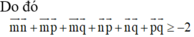
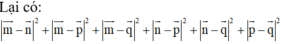
Đáp án đúng : B