
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) `(x-3)^4 >=0`
`2.(x-3)^4>=0`
`2.(x-3)^4-11 >=-11`
`=> A_(min)=-11 <=> x-3=0<=>x=3`
2) `|5-x|>=0`
`-|5-x|<=0`
`-3-|5-x|<=-3`
`=> B_(max)=-3 <=>x=5`.
Bài 1:
Ta có: \(\left(x-3\right)^4\ge0\forall x\)
\(\Leftrightarrow2\left(x-3\right)^4\ge0\forall x\)
\(\Leftrightarrow2\left(x-3\right)^4-11\ge-11\forall x\)
Dấu '=' xảy ra khi x=3

\(A=\left|x-2\right|+\dfrac{4}{7}\ge\dfrac{4}{7}\)
dấu"=" xảy ra \(< =>x=2\)
Tìm giá trị nhỏ nhất của:A=/2.5-x/+5,8
Tìm giá trị lớn nhất của:B=2-/x+2/3/ (là 2 phần 3 nha mấy bạn)

ta có: /2,5-x/\(\ge\)0, nên A= /2,5-x/ + 5,8 \(\ge\)5,8
vậy giá trị nn của A là 5,8, A=5,8 khi /2,5-x/=0
<=> x=2,5
ta có: /x+2/3/ \(\ge\)0 nên B= 2 - /x+2/3/ \(\le\)2
vậy gtln của B là 2, B=2 khi /x+2/3/=0 <=> x= -2/3

1) \(A=\frac{\left|x-2016\right|+2017}{\left|x-2016\right|+2018}=\frac{\left|x-2016\right|+2018-1}{\left|x-2016\right|+2018}=1-\frac{1}{\left|x-2016\right|+2018}\)
\(A\)nhỏ nhất nên \(\frac{1}{\left|x-2016\right|+2018}\)lớn nhất nên \(\left|x-2016\right|+2018\)dương nhỏ nhất.
mà \(\left|x-2016\right|+2018\ge2018\)
Dấu \(=\)khi \(x=2016\).
Vậy \(minA=1-\frac{1}{2018}=\frac{2017}{2018}\)đạt tại \(x=2016\).
2) \(x-2xy+y=0\)
\(\Leftrightarrow x\left(1-2y\right)+\frac{1}{2}-y-\frac{1}{2}=0\)
\(\Leftrightarrow\left(2x+1\right)\left(1-2y\right)=1=1.1=\left(-1\right).\left(-1\right)\)
Từ đây xét 2 trường hợp nha. Ra kết quả cuối cùng là: \(\left(x,y\right)\in\left\{\left(0,0\right),\left(1,1\right)\right\}\).

\(A=-\left|x-3.5\right|+0.5\le0.5\forall x\)
Dấu '=' xảy ra khi x=3,5
\(B=-\left|1.4-x\right|-2\le-2\forall x\)
Dấu '=' xảy ra khi x=1,4

ta có: |x - 2016 | = x- 2016 nếu x \(\ge\) 2016
|x - 2016| = -x + 2016 nếu x \(\le\) 2016
|x - 1| = x - 1 nếu x \(\ge\) 1 và |x - 1| = - x + 1 nếu x \(\le\) 1
+) nếu x \(\le\) 1 => |x - 2016 | + |x - 1| = - x + 2016 - x + 1 = -2x + 2017 \(\ge\) (-2). 1 + 2017 = 2015 (1)
+) Nếu 1 \(\le\) x \(\le\) 2016 => | x - 2016 | + |x - 1| = - x + 2016 + x - 1 = 2015 (2)
+) Nếu x \(\ge\) 2016 => |x - 2016| + |x - 1| = x - 2016 + x - 1 = 2x - 2017 \(\ge\) 2. 2016 - 2017 = 2015 (3)
Từ (1)(2)(3) => |x - 2016| + |x -1| \(\ge\) 2015
vậy giá trị nhỏ nhất của |x - 2016| + |x -1| bằng 2015 khi x = 1 hoặc x = 2016

Ta có : \(\left|x-5\right|\ge0\forall x\)
\(\left|y-3\right|\ge0\forall y\)
\(\Rightarrow50+\left|x-5\right|+\left|y-3\right|\ge50\)
\(\Rightarrow\text{ Min A = 50}\)
Dấu "=" xảy ra khi
\(\hept{\begin{cases}\left|x-5\right|=0\\\left|y-3\right|=0\end{cases}\Rightarrow\hept{\begin{cases}x-5=0\\y-3=0\end{cases}\Rightarrow}\hept{\begin{cases}x=5\\y=3\end{cases}}}\)
Vậy GTNN của A = 50 khi \(\hept{\begin{cases}x=5\\y=3\end{cases}}\)

+)Với \(x\le2016\)
=>\(A=\left|x-2016\right|+x-1=2016-x+x-1=2015\)
+)Với x>2016
=>\(A=\left|x-2016\right|+x-1=x-2016+x-1=2x-2017>2015\)
So sánh 2 trường hợp ta thấy A đạt giá trị nhỏ nhất là 2015 khi \(x\le2016\)
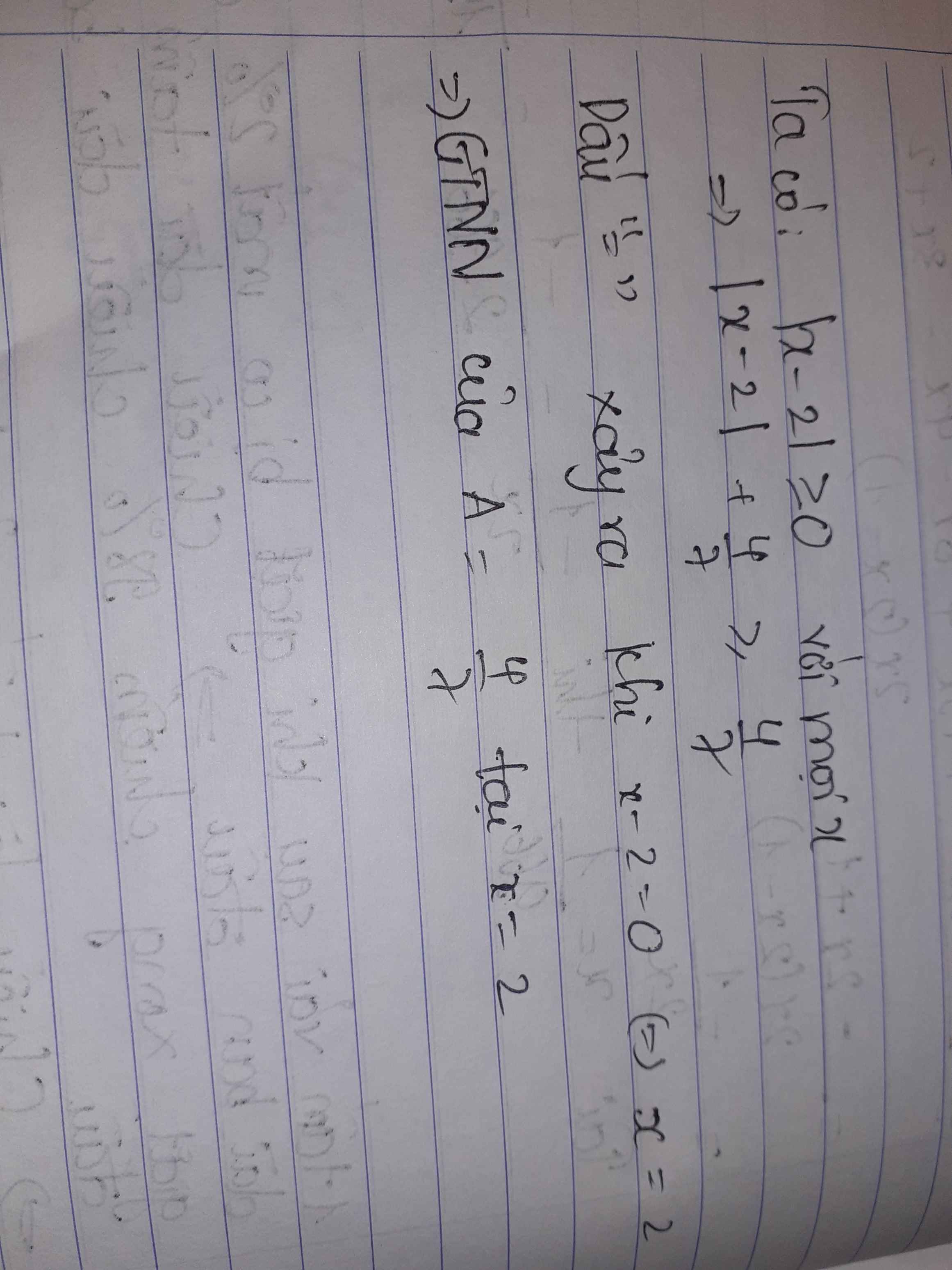
bó tay