AA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 2 2022
Hướng dẫn: đặt \(A=\dfrac{y^4}{\left(x^2+y^2\right)\left(x+y\right)}+\dfrac{z^4}{\left(y^2+z^2\right)\left(y+z\right)}+\dfrac{x^4}{\left(z^2+x^2\right)\left(z+x\right)}\)
Khi đó \(F-A=x-y+y-z+z-x=0\Rightarrow F=A\)
\(\Rightarrow2F=F+A=\sum\dfrac{x^4+y^4}{\left(x^2+y^2\right)\left(x+y\right)}\ge\sum\dfrac{\left(x^2+y^2\right)^2}{2\left(x^2+y^2\right)\left(x+y\right)}\ge\sum\dfrac{\left(x+y\right)^2\left(x^2+y^2\right)}{4\left(x^2+y^2\right)\left(x+y\right)}\)
\(\Rightarrow2F\ge\dfrac{x+y+z}{2}\Rightarrow F\ge\dfrac{x+y+z}{4}\)
23 tháng 2 2021
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
6 tháng 1 2022
a: \(P=\left(\dfrac{2+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}+1}{1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để P nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
hay \(x\in\left\{0;4;9\right\}\)
AA
7
8 tháng 4 2021
Ta có x \(\ge\) 3 => \(\dfrac{1}{x}\) \(\ge\dfrac{1}{3}\)=> x + \(\dfrac{1}{x}\ge\dfrac{4}{3}\)=>\(\min\limits_{ }\)=\(\dfrac{4}{3}\) tại x=0
AH
Akai Haruma
Giáo viên
31 tháng 5 2023
Lời giải:
ĐKXĐ: $x\geq 0; x\neq 1$
\(P=\frac{x+\sqrt{x}-(x+2)}{\sqrt{x}+1}:\left[\frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}+1)(\sqrt{x}-1)}+\frac{\sqrt{x}-4}{(\sqrt{x}-1)(\sqrt{x}+1)}\right]\)
\(=\frac{\sqrt{x}-2}{\sqrt{x}+1}:\frac{x-\sqrt{x}+\sqrt{x}-4}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{\sqrt{x}-2}{\sqrt{x}+1}:\frac{x-4}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{\sqrt{x}-2}{\sqrt{x}+1}.\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(\sqrt{x}-2)(\sqrt{x}+2)}\)
\(=\frac{\sqrt{x}-1}{\sqrt{x}+2}=1-\frac{3}{\sqrt{x}+2}\)
Với mọi $x\geq 0; x\neq 1$ thì $\sqrt{x}+2\geq 2$
$\Rightarrow \frac{3}{\sqrt{x}+2}\leq \frac{3}{2}$
$\Rightarrow P=1-\frac{3}{\sqrt{x}+2}\geq 1-\frac{3}{2}=\frac{-1}{2}$
Vậy $P_{\min}=\frac{-1}{2}$ khi $x=0$
25 tháng 12 2021
Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2
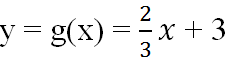
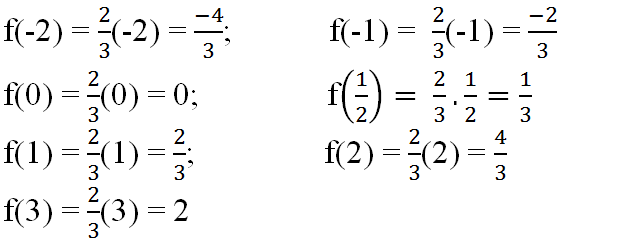
Giá trị nhỏ nhất là 9/4
\(\dfrac{9}{4\:}\)