Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔADH vuông tại H và ΔBCK vuông tại K có
AD=BC(ABCD là hình thang cân)
\(\widehat{D}=\widehat{C}\)(ABCD là hình thang cân)
Do đó: ΔADH=ΔBCK(cạnh huyền-góc nhọn)
Suy ra: DH=CK(hai cạnh tương ứng)
b) Xét ΔAHC vuông tại H và ΔBKD vuông tại K có
AC=BD(ABCD là hình thang cân)
AH=BK(ΔADH=ΔBCK)
Do đó: ΔAHC=ΔBKD(Cạnh huyền-cạnh góc vuông)
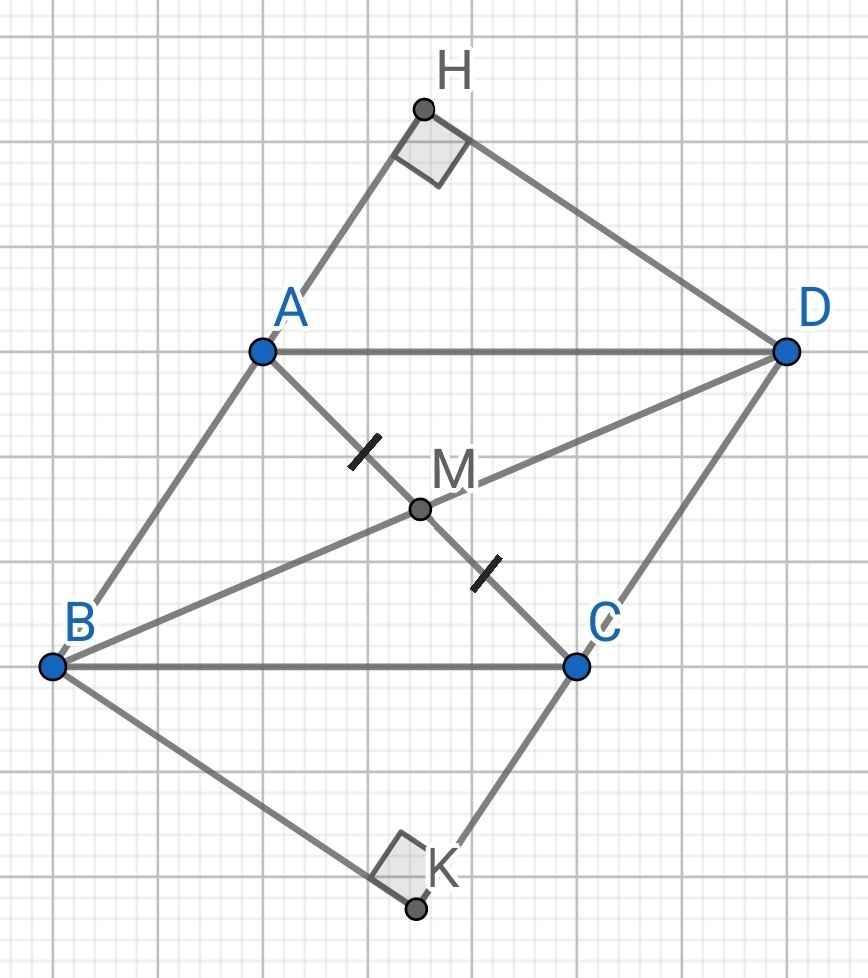a) Do BM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của AC
Do D và B đối xứng qua M (gt)
⇒ M là trung điểm của BD
Tứ giác ABCD có:
M là trung điểm của AC (cmt)
M là trung điểm của BD (cmt)
⇒ ABCD là hình bình hành
b) Do ABCD là hình bình hành (cmt)
⇒ AB // CD
Mà DH ⊥ AB
⇒ DH ⊥ AC
c) Do ABCD là hình bình hành
⇒ AB // CD
Mà BK ⊥ CD
⇒ BK ⊥ AB
⇒ ∠KBH = 90⁰
Tứ giác BHDK có:
∠BKD = ∠KBH = ∠BHD = 90⁰
⇒ BHDK là hình chữ nhật
Mà M là trung điểm BD
⇒ M là trung điểm của HK
⇒ M, H, K thẳng hàng
Do đó chứng minh MH ⊥ MK là sai. Em xem lại đề ở câu c nhé
a: Xét ΔBMC vuông tại M và ΔDNC vuông tại N có
góc B=góc D
=>ΔBMC đồng dạng vớiΔDNC
b: Bạn ghi lại đề đi bạn
a: Xét tứ giác AMIN có \(\widehat{AMI}=\widehat{ANI}=\widehat{NAM}=90^0\)
nên AMIN là hình chữ nhật
b: IN=3cm
nên AM=3cm
IM=4cm
nên AN=4cm
Xét ΔABC có
I là trung điểm của BC
IM//AC
Do đó: M là trung điểm của AB
=>AB=6cm
Xét ΔABC có
I là trung điểm của BC
IN//AB
Do đó: N là trung điểm của AC
hay AC=8cm
\(S_{ABC}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: Xét tứ giác ADCI có
N là trung điểm của AC
N là trung điểm của DI
Do đó: ADCI là hình bình hành
mà IA=IC
nên ADCI là hình thoi
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
CD là phângíac
=>AD/AC=DB/CB
=>AD/3=DB/5=(AD+DB)/(3+5)=8/8=1
=>AD=3cm; BD=5cm
a: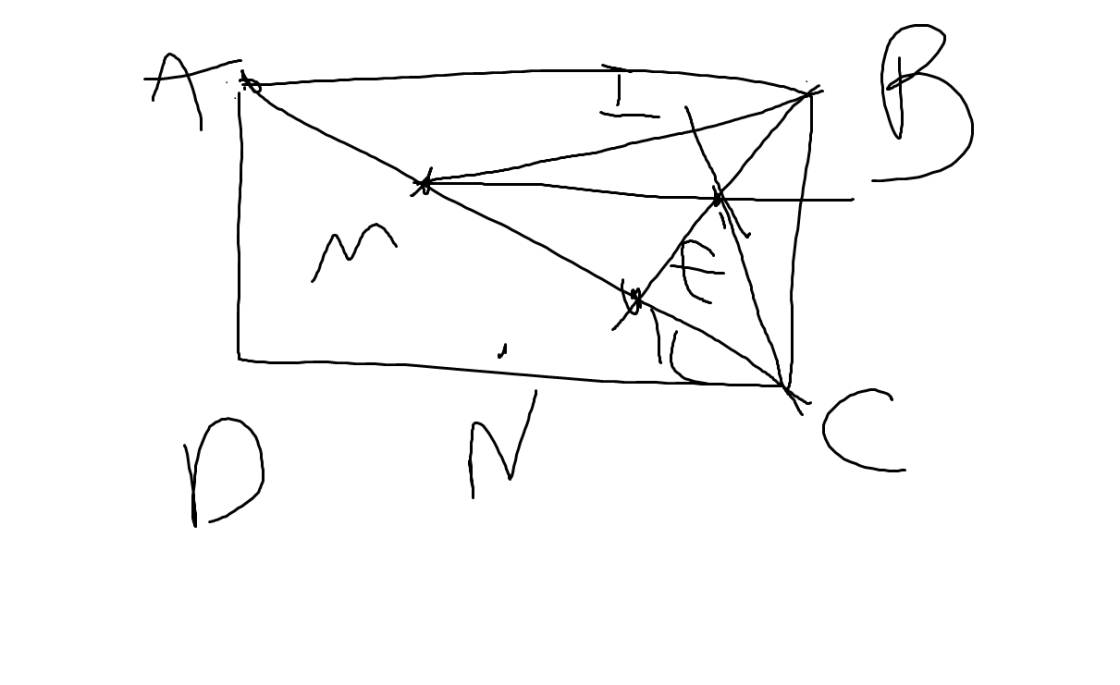 
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB