Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

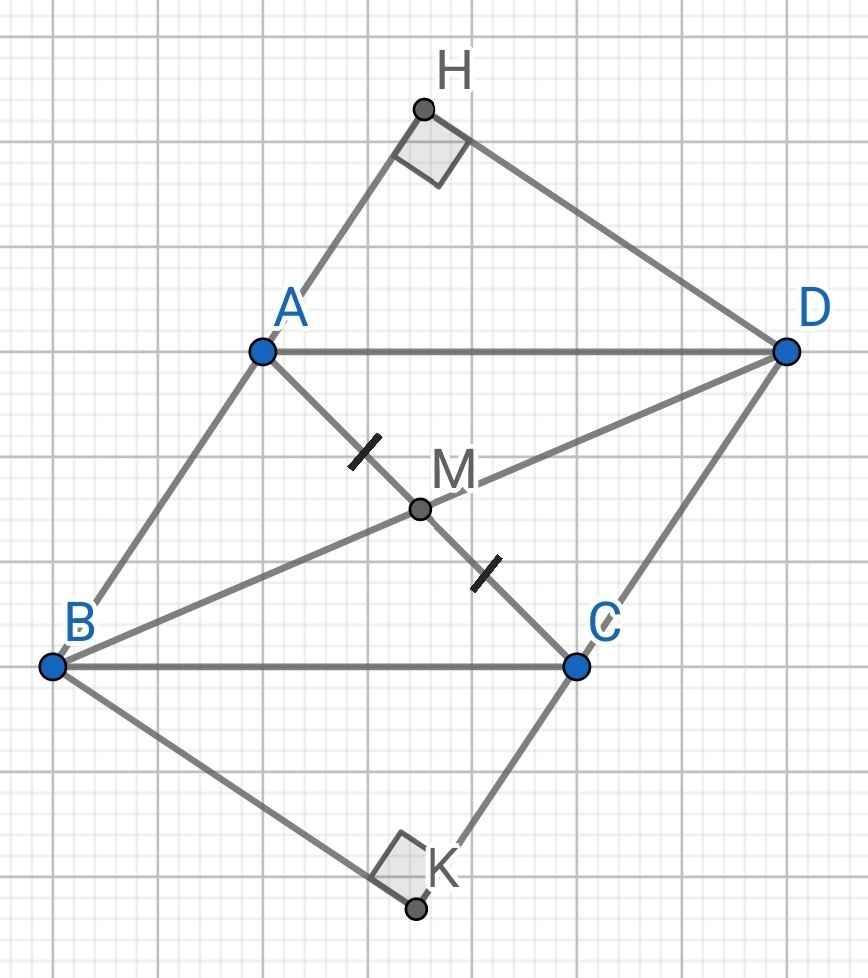 a) Do BM là đường trung tuyến của ∆ABC (gt)
a) Do BM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của AC
Do D và B đối xứng qua M (gt)
⇒ M là trung điểm của BD
Tứ giác ABCD có:
M là trung điểm của AC (cmt)
M là trung điểm của BD (cmt)
⇒ ABCD là hình bình hành
b) Do ABCD là hình bình hành (cmt)
⇒ AB // CD
Mà DH ⊥ AB
⇒ DH ⊥ AC
c) Do ABCD là hình bình hành
⇒ AB // CD
Mà BK ⊥ CD
⇒ BK ⊥ AB
⇒ ∠KBH = 90⁰
Tứ giác BHDK có:
∠BKD = ∠KBH = ∠BHD = 90⁰
⇒ BHDK là hình chữ nhật
Mà M là trung điểm BD
⇒ M là trung điểm của HK
⇒ M, H, K thẳng hàng
Do đó chứng minh MH ⊥ MK là sai. Em xem lại đề ở câu c nhé

a: Xét tứ giác AMIN có \(\widehat{AMI}=\widehat{ANI}=\widehat{NAM}=90^0\)
nên AMIN là hình chữ nhật
b: IN=3cm
nên AM=3cm
IM=4cm
nên AN=4cm
Xét ΔABC có
I là trung điểm của BC
IM//AC
Do đó: M là trung điểm của AB
=>AB=6cm
Xét ΔABC có
I là trung điểm của BC
IN//AB
Do đó: N là trung điểm của AC
hay AC=8cm
\(S_{ABC}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: Xét tứ giác ADCI có
N là trung điểm của AC
N là trung điểm của DI
Do đó: ADCI là hình bình hành
mà IA=IC
nên ADCI là hình thoi

B C A M H K N D O I
a) Xét tứ giác BHMK có 3 góc vuông nên nó là hình chữ nhật.
Khi đó hai đường chéo bằng nhau nên BM = HK.
b) Xét tam giác ABC có M là trung điểm AC, MK // AB nên MK là đường trung bình.
Vậy thì K là trung điểm BC.
Xét tứ giác BMCN có K là trung điểm hai đường chéo nên nó là hình bình hành.
Lại có MN vuông góc BC nên BMCN là hình thoi.
Dễ thấy rằng MK = AB/2 hay MN = AB.
Để hình thoi BMCN là hình vuông thì MN = BC hau AB = BC.
Vậy tam giác ABC là tam giác vuông cân tại B thì BMCN là hình vuông.
c) Ta có BHMK là hình chữ nhật nên BM giao HK tại trung điểm mỗi đường.
Dễ thấy tứ giác ABNM có AB song song và bằng NM nên nó là hình bình hành.
Vậy nên BM giao AM tại trung điểm mỗi đoạn.
Từ đó ta có BM, HK, AN đồng quy tại trung điểm mỗi đoạn.
d) Gọi giao điểm của BM, HK và AN làO, giao của BM và AK là I.
Ta có: do KM // AB, áp dụng Talet:
\(\frac{IM}{BI}=\frac{MK}{AB}=\frac{1}{2}\Rightarrow\frac{IM}{BO+OI}=\frac{1}{2}\Rightarrow\frac{IM}{IM+OI+OI}=\frac{1}{2}\)
\(\Rightarrow IM=2OM\)
Áp dụng Talet cho tam giác AND và ADC ta có:
\(\frac{OI}{DN}=\frac{AI}{AD}=\frac{IM}{DC}\Rightarrow\frac{OI}{DN}=\frac{IM}{DC}\Rightarrow DC=2ND\)