NP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 7 2021
bạn đăg tách ra cho m.n cùng giúp nhé
Bài 2 :
a, \(A=\left|2x-4\right|+2\ge2\)
Dấu ''='' xảy ra khi x = 2
Vậy GTNN A là 2 khi x = 2
b, \(B=\left|x+2\right|-3\ge-3\)
Dấu ''='' xảy ra khi x = -2
Vậy GTNN B là -3 khi x = -2
3 tháng 9 2021
\(\left|x-\dfrac{2}{3}\right|-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)
31 tháng 7 2023
\(\left|x+2017\right|+\left|x-2\right|=\left|x+2017\right|+\left|2-x\right|>=\left|x+2017+2-x\right|=2019\)
=>A=1/|x+2017|+|x-2|<=1/2019
Dấu = xảy ra khi -2017<=x<=2
S6
0
NC
2
21 tháng 3 2022
lx+2017l +lx-2l > 0
Xét :
|x+2017| > 2017 với mọi x . Dấu bằng xảy ra khi và chỉ khi x = 0
|x-2| > 2 với mọi x. Dấu "=" xảy ra khi và chỉ khi x = 0
Vậy giá trị lớn nhất của A \(=\frac{1}{2019}\) khi x = 0
21 tháng 3 2022
\(A=\frac{1}{\left|x+2017\right|+\left|x-2\right|}\)
TH1 : \(x\ge2\)\(\Rightarrow\left|x+2017\right|=x+2017\)
\(\left|x-2\right|=x-2\)
\(\Rightarrow A=\frac{1}{2x+2015}\)Do \(x\ge2\Rightarrow2x+2015\ge2019\)
\(\Rightarrow A\le\frac{1}{2019}\)Dấu '' = '' xảy ra khi x = 2
TH2 : \(x\le-2017\)\(\Rightarrow\left|x+2017\right|=-x-2017\)
\(\left|x-2\right|=2-x\)
\(\Rightarrow A=\frac{1}{-2x-2015}\)
\(x\le-2017\Rightarrow-2x\ge4034\)
\(\Rightarrow-2x-2015\ge2019\)
\(\Rightarrow A\le\frac{1}{2019}\). Dấu '' = '' xảy ra \(\Leftrightarrow x=-2017\)
TH3 : \(-2017< x< 2\)\(\Rightarrow\left|x+2017\right|=x+2017\)
\(\left|x-2\right|=2-x\)
\(\Rightarrow A=\frac{1}{2019}\)
Vậy GTLN của A là \(\frac{1}{2019}\)
Dấu '' = '' xảy ra \(\Leftrightarrow-2017\le x\le2\)
22 tháng 10 2021
a, Áp dụng t/c dtsbn:
\(5x=7y\Rightarrow\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{y-x}{5-7}=\dfrac{2}{-2}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-7\\y=-5\end{matrix}\right.\)
b, Áp dụng t/c dtsbn:
\(\dfrac{x}{y}=\dfrac{7}{2}\Rightarrow\dfrac{x}{7}=\dfrac{y}{2}=\dfrac{x+y}{7+2}=\dfrac{-27}{9}=-3\\ \Rightarrow\left\{{}\begin{matrix}x=-21\\y=-6\end{matrix}\right.\)
c, \(\dfrac{x}{32}=\dfrac{2}{x}\Rightarrow x^2=2\cdot32=64\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d, \(\left|x+\dfrac{1}{3}\right|-2=\dfrac{1}{2}\Rightarrow\left|x+\dfrac{1}{3}\right|=\dfrac{5}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=\dfrac{5}{2}\\x+\dfrac{1}{3}=-\dfrac{5}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{13}{6}\\x=-\dfrac{17}{6}\end{matrix}\right.\)
D
2
22 tháng 3 2020
Tìm GTNN của biểu thức B = I x-2017 I + I x-1 I
có |x-2017|luôn\(\ge0\forall x\in Q\)
cũng có |-1|luôn\(\ge0\forall x\in Q\)
=>I x-2017 I + I x-1 I\(\ge0\forall x\in Q\)
=> I x-2017 I + I x-1 I=|x-2017|+|1-x|=|x-2017+1-x|=2016
dấu''='' xảy ra <=>(x-2017)(1-x)=0
TH1:
=>\(\orbr{\begin{cases}x-2017\ge0\\1-x\le0\end{cases}}\)
TH2:
=> \(\orbr{\begin{cases}x-2017\le0\\1-x\ge0\end{cases}}\)
tự làm típ ! xét 2 TH thấy cái nào mà nó vô lí thì đánh vô lí chọn TH còn lại nhé !
ST
0
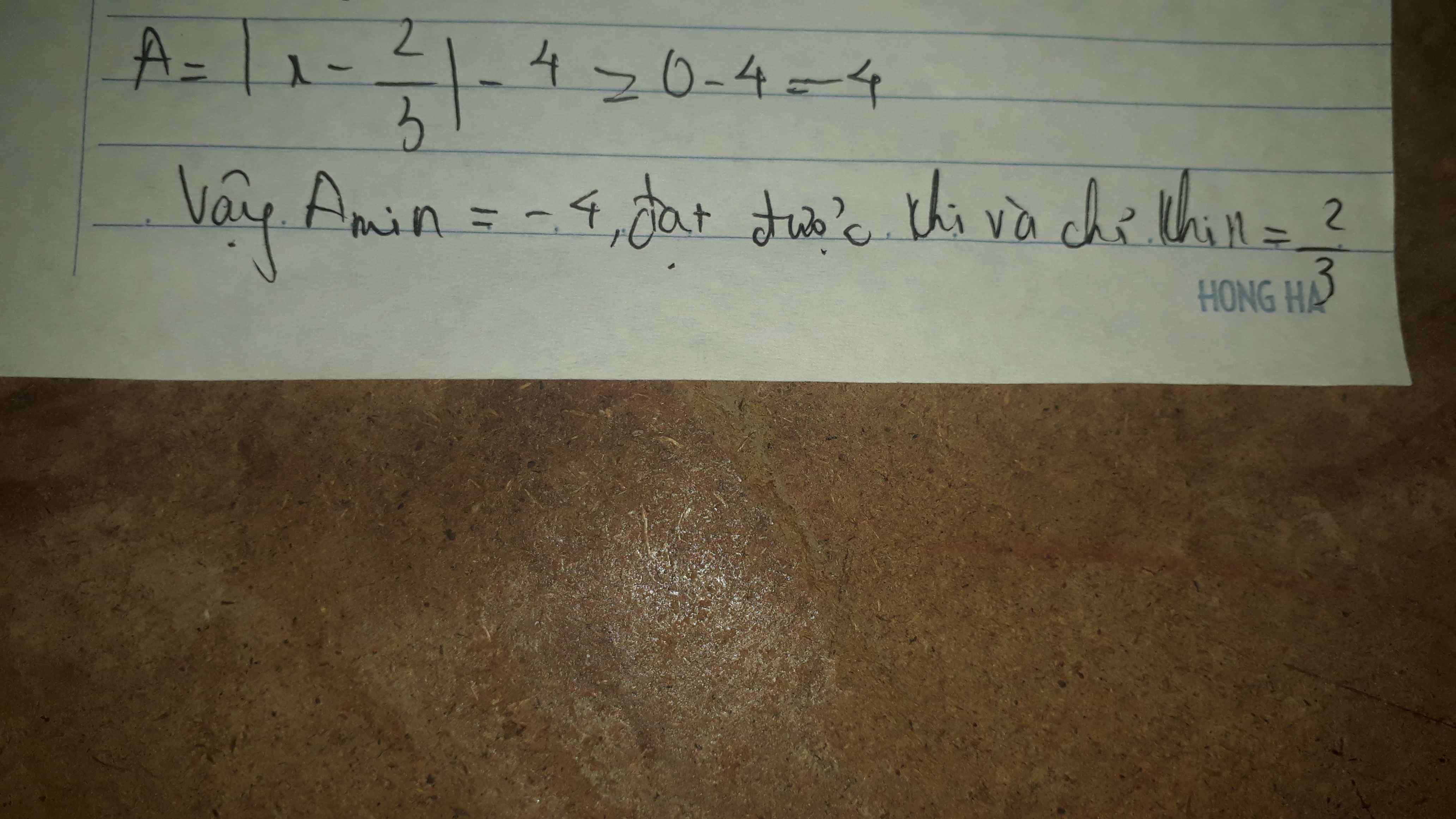
không biết