
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có f ' x = - m 2 + m + 1 x + 1 2 > 0
Suy ra f(x) là hàm đồng biến trên [0;1]
Do đó f 0 ≤ f x ≤ f 1 hay
- m 2 + m ≤ f x ≤ 1 2 - m 2 + m + 1
Khi đó
m i n x ∈ 0 ; 1 f x = - m 2 + m = - 2 ⇔ m = - 1 m = 2
Đáp án A

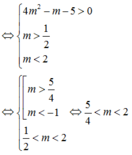

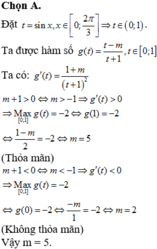

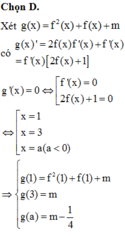
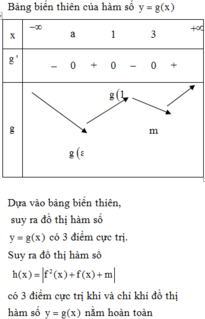
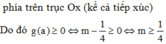
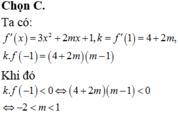

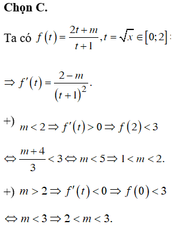


Đáp án C
Ta có lim x → 1 f ( x ) = lim x → 1 3 x + 1 - 2 x - 1 = lim x → 1 3 3 x + 1 + 2 = 3 4 , vì 3 x - 3 = 3 x + 1 - 2 3 x + 1 + 2
Để hàm số liên tục tại điểm x 0 = 1 ⇔ lim x → 1 f x = f 1 ⇔ m = 3 4 .